Ejercicios de Matemáticas Aplicadas a las Ciencias Sociales II ( opciones A y B ), resueltos y comentados, correspondientes a las pruebas PAU de Septiembre de 2016, en Madrid

[ 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 ]

El tiempo, en meses, de permanencia de un socio en un cierto club deportivo, se puede aproximar por una variable aleatoria (...)

ENUNCIADO. El tiempo, en meses, de permanencia de un socio en un cierto club deportivo, se puede aproximar por una variable aleatoria con distribución normal de media desconocida $\mu$ y desviación típica/estándar $\sigma=9$ meses.
a) Se toma una muestra aleatoria simple de $100$ personas que han sido socias de ese club, resultando una estancia media de $\bar{x}=8'1$ meses. Determínese un intervalo de confianza al $90\,\%$ para la media de la población $\mu$
b) Sabiendo que para una muestra aleatoria simple de $144$ personas se ha obtenido el intervalo de confianza $(7'766\,,\,10'233)$ para la media de la población $\mu$, determínese el nivel de confianza con el que se obtuvo dicho intervalo.

SOLUCIÓN.

a)
Denotemos por $X$ a la variable aleatoria de la población "tiempo de permanencia en el club". Sabemos que $X \sim N(\mu\,,\,9)$ ( en meses ), entonces un intervalo de confianza para la estimación de la media de la población $\mu$ es $(\bar{x}-E\,,\,\bar{x}+E)$, donde $\bar{x}=8'1$ meses y $E$ es el máximo error cometido en la estimación ( amplitud del intervalo de confianza ), que viene dado por $E=z_{\alpha/2}\cdot \dfrac{\sigma}{\sqrt{n}}$ y cuyo valor vamos a calcular a continuación. Como el nivel de confianza es $1-\alpha=0{,}90$, luego $\alpha=0{,}10$ y por tanto $\alpha/2=0{,}05$; entonces $P\{Z \le z_{\alpha/2}\}=1-0{,}05=0{,}95$, por lo que consultando en las tablas de la distribución de probabilidad normal tipificada $N(0\,,\,1)$ encontramos el siguiente valor de la abscisa $z_{\alpha/2}\approx 1'64$

Así, $E=1'64 \cdot \dfrac{9}{\sqrt{100}}\approx 1'476$. Y, por consiguiente, el intervalo de confianza pedido para la media de la población es $(8'1-1'476\,,\,8'1+1'476)$ esto es $(6'624\,,\,9'576)$. En buena lógica, vamos ahora a aproximar el extremo inferior por defecto y el extremo superior por exceso, por lo que podemos concluir que el intervalo de confianza pedido es $(6\;,\;10)$ meses.

b)
Recordemos que la amplitud del intervalo de confianza viene dado por $E=z_{\alpha/2}\cdot \dfrac{\sigma}{\sqrt{n}}$. En este apartado del problema, partimos de los siguientes datos: $\sigma=9$ minutos, $n=144$ y $E =\dfrac{10'233-7'766}{2}=1'2335$ minutos. entonces $1'2335=z_{\alpha/2}\cdot \dfrac{9}{\sqrt{144}} \Rightarrow z_{\alpha/2}\approx 1'64$. Consultando ahora las tablas de la función de distribución normal tipificada $N(0,1)$ encontramos $F(1'64) \equiv P\{ Z \le z_{\alpha/2} \}=P\{ Z \le 1'64\}=1-\alpha/2=0'9495$.

Entonces, si $1-\alpha/2=0'9495=94'95\,\%$, el nivel de riesgo en la estimación es $\alpha=2\cdot (1-0'9495)=0'101$, de donde se sigue que el nivel de confianza $1-\alpha$ es igual a $1-0'101=0'899=89'9\,\%$
$\square$

Para efectuar un diagnóstico (...)

ENUNCIADO. Para efectuar cierto diagnóstico, un hospital dispone de dos escáneres, a los que denotamos por $A$ y $B$. El $65\,\%$ de las pruebas de diagnóstico que se llevan a cabo en ese hospital se realizan usando el escáner $A$, el resto con el escáner $B$. Se sabe además que el diagnóstico efectuado usando el escáner $A$ es erróneo en un $5\,\%$ de los casos, mientras que el diagnóstico efectuado usando el escáner $B$ es erróneo en un $8\,\%$ de los casos. Calcúlese la probabilidad de que:
a) El diagnóstico correspondiente a una prueba ( elegida al azar ) efectuada a un paciente en ese hospital sea erróneo
b) El diagnóstico se haya efectuado usando el escáner $A$, sabiendo que ha sido erróneo.

SOLUCIÓN.
a)
Denotemos por $E$ al suceso aleatorio "realizar una prueba errónea"; y, por $A$ y $B$, a los sucesos aleatorios "hacer una prueba con el escáner $A$" y "hacer una prueba con el escáner $B$", respectivamente. Entonces, $$E=(E \cap A)\cup (E \cap B)$$ y como los sucesos $E \cap A$ y $E \cap B$ son incompatibles ( su intersección es vacía ), podemos escribir $$P(E)=P(E \cap A)+P(E \cap B)$$ Ahora bien, por la definición de probabilidad de sucesos condicionados, $P(E \cap A)=P(E|A)P(A)$ y $P(E \cap B)=P(E|B)P(B)$ luego $$P(E)=P(E|A)P(A)+P(E|B)P(B) \quad \text{(teorema de la Probabilidad Total)}$$ Poniendo pues los datos, llegamos a $$P(E)=0,65\cdot 0,05 + 0,35\cdot 0,08=0,0605$$

b)
Por el teorema de Bayes, podemos escribir $$P(A|E)=\dfrac{P(E|A)P(A)}{P(E)}$$ y con los datos de que disponemos, $$P(A|E)=\dfrac{0,65\cdot 0,05}{0,0605}\approx 0,2893$$
$\square$

Se considera la función (...)

ENUNCIADO. Se considera la función real de variable real $$f(x)=\dfrac{x^2-3}{x^2-9}$$
a) Calcúlense sus asíntotas
b) Determínense los intervalos de crecimiento y decrecimiento de la función

SOLUCIÓN.
a)
Podemos expresar la función de la forma $$f(x)=\dfrac{x^2-3}{(x-3)(x+3)}$$ con lo cual vemos que el denominador ( y no el numerador ) se anula para $x=-3$ y $x=3$, así que la función tiene dos asíntotas verticales: $$\text{a.v}_1:x=-3$$ y $$\text{a.v}_2:x=3$$ Veamos ahora si tiene alguna asíntota oblicua ( incluidas las posibles asíntotas horizontales en ese grupo ).

Una asíntota oblicua se escribe de la forma $y=mx+k$, donde $$\displaystyle m\overset{\text{def}}{=}\lim_{x \rightarrow \pm \infty}\,f'(x)=\lim_{x \rightarrow \pm \infty}\,\dfrac{f(x)}{x}$$ Así, $\displaystyle m=\lim_{x \rightarrow \pm \infty}\,\dfrac{x^2-3}{x(x-3)(x+3)}=0$ por ser el grado del polinomio del denominador mayor que el del polinomio del numerador. La única asíntota que encontramos, pues, es una asíntota horizontal, del tipo $y=k$.

Procedemos a calcular el valor de $k$: $\displaystyle k\overset{\text{def}}{=}\lim_{x \rightarrow \pm \infty}\,(f(x)-mx)=\lim_{x \rightarrow \pm \infty}\,f(x)=\lim_{x \rightarrow \pm \infty}\,\dfrac{x^2-3}{x^2-9}=1$, por ser iguales los grados de los polinomios del numerador y denominador, siendo los coeficientes de mayor grado igual a $1$ en sendos polinomios. Por consiguiente, la ecuación de la recta asíntota horizontal que acabamos de encontrar es $\text{a.h.}:y=1$


b)
Para calcular los intervalos de crecimiento y decrecimiento, vamos a ver primero si la función tiene algún extremo relativo. Imponiendo la condición necesaria de existencia de extremos relativos $$f'(x)=0$$ vemos que $$\dfrac{2x(x^2-9)-2x(x^2-3)}{(x^2-9)^2}=0 \Leftrightarrow x=0$$ Investiguemos ahora de qué tipo de extremo relativo se trata. A la izquierda de $x^*=0$, en puntos muy cercanos ( pongamos que, por ejemplo, en $x=-1$) la primera derivada tiene signo positivo; y, a la derecha, en puntos muy cercanos ( por ejemplo en $x=1$ ) tiene signo negativo, de lo cual se deduce que el extremo relativo encontrado corresponde a un máximo relativo.

Con la información recogida hasta este punto podemos ver que $$\displaystyle \lim_{x \rightarrow -3^{-}}\,f(x)=+\infty$$ $$\displaystyle \lim_{x \rightarrow -3^{+}}\,f(x)=-\infty$$ $$\displaystyle \lim_{x \rightarrow 3^{-}}\,f(x)=-\infty$$ y $$\displaystyle \lim_{x \rightarrow 3^{+}}\,f(x)=+\infty$$
También es útil conocer el valor de las raíces de la función: $$f(x)=0 \Leftrightarrow x^2-3=0 \Leftrightarrow x=\left\{\begin{matrix}-\sqrt{3}\\ \\ \sqrt{3}\end{matrix}\right.$$

Así, podemos bosquejar el siguiente gráfico para la función:

con lo cual podemos escribir los intervalos de crecimiento: $(-\infty,-3)$ y $(-3,0)$, así como los de decrecimiento: $(0,3)$ y $(3,+\infty)$
$\square$

Se considera la función real de variable real (...)

ENUNCIADO. Se considera la función real de variable real $$f(x)=\left\{\begin{matrix}x^2+2x & \text{si} & x \prec 0 \\ -x^2+3x & \text{si} & x \ge 0 \end{matrix}\right.$$
a) Estúdiese la continuidad y la derivabilidad de la función
b) Determínense los valores de $a \in \mathbb{R}$ para los cuales la pendiente de la recta tangente a la gráfica de $f(x)$ en el punto de abscisa $x=a$ es $-2$. Calcúlese, para cada valor de $a$ obtenido, la recta tangente a la gráfica de $f(x)$ en el punto de abscisa $x=a$

SOLUCIÓN.
a)
Estudio de la continuidad:
Las dos tramos polinómicos en que está definida la función son continuos, por ser polinomios. El único punto donde podría haber problemas de continuidad es en $x=0$, sin embargo la función también es continua en dicho punto. En efecto, $\displaystyle \lim_{x\rightarrow 0^-}f(x)=\displaystyle \lim_{x\rightarrow 0^+}f(x)=0$, luego el límite global existe y su valor es $\displaystyle \lim_{x\rightarrow 0}f(x)=0$; y, por otra parte, el valor de dicho límite es igual al valor de la función en $x=0$, $f(0)=0$. En consecuencia la función es continua en todos los puntos del dominio de definición, que es todo el conjunto $\mathbb{R}$.

Estudio de la derivabilidad:
Los dos tramos de la función son derivables en todos los puntos, ya que son polinomios. El único punto que podría presentar problemas de derivabilidad es en $x=0$ ( en punto de engarce de los dos tramos ). Veamos si la función es derivable en $x=0$. Para que lo sea, al calcular los límites que definen la derivada, por la izquierda y por la derecha de $x=0$, deberían dar el mismo valor. Veamos si es así: $$\displaystyle \lim_{\Delta x\rightarrow 0}\dfrac{f(0)-f(0-\Delta x)}{\Delta x}=(x^2+2x)'|_{x=0}=(2x+2)'|_{x=0}=2\cdot 0+2=2$$ por el contrario $$\displaystyle \lim_{\Delta x\rightarrow 0}\dfrac{f(0+\Delta x)-f(0)}{\Delta x}=(-x^2+3x)'|_{x=0}=(-2x+3)'|_{x=0}=-2\cdot 0+3=3$$ Al no coincidir dichos límites, no existe la derivada de $f(x)$ en $x=0$; en otras palabras, no podemos trazar la recta tangente a la gráfica de la función en el punto $x=0$. Así pues, el dominio de derivabilidad de $f(x)$ es $\mathbb{R}\setminus \{0\}$

b)
Procedemos a investigar en qué puntos de $\mathbb{R}$ la recta tangente a la gráfica de la función tiene pendiente negativa. El primer tramo de la función, esto es el polinomio $x^2+2x$ ( definido para todos los números reales negativos ) presenta un mínimo relativo en $x=-1$, ya que ésta es la abscisa del vértice de la parábola dada por dicho polinomio. Por otra parte, el segundo tramo, $-x^2+3x$, que también es un polinomio ( definido para el cero y todos los números reales positivos ) presenta un máximo relativo ( la parábola asociada a dicho tramo polinómico tiene coeficiente principal negativo ) en $x=3/2$, que es la abscisa el vértice de dicha parábola. Nota: También podemos deducir las abscisas de dichos extremos relativos, derivando e igualando a cero.

Entonces, los intervalos de decrecimiento de la función, donde la pendiente de la recta tangente es negativa, son: $I_1=(-\infty,-1)$ e $I_2=(3/2,+\infty)$, con lo cual encontraremos dos valores, $a$, del dominio de derivabilidad de $f(x)$ que cumplen que la pendiente de la recta tangente a la gráfica de la función $f(x)$ es igual a $-2$; uno de ellos ha de ser menor que $-1$, pues está en $I_1$, y el otro ha de ser mayor que $3/2$, pues está en $I_2$. Distinguimos pues los siguientes casos.

Caso I:
La pendiente de la recta tangente en un punto $x=a$ situado a la izquierda de $-1$ ( esto es, del intervalor $I_1$ ) ha de ser igual a $-2$ (enunciado), y dicho valor corresponde a la derivada de la función en dicho punto, $f'(a)$. Como para $x\prec -1$, $f'(x)=2x+2$, tenemos que $(2x+2)_{x=a}=-2$ y por tanto $$2a+2=-2$$ de donde deducimos que $a=-2$

A continuación, vamos a escribir la ecuación de la recta tangente a la gráfica de la función en dicho punto $a=-2$, que designaremos por $\text{r.t.}_1$. Sabemos que la ecuación de dicha recta es de la forma $y=mx+k$, y como la pendiente de dicha recta es $m=-2$, nos queda $y=-2x+k$. Para determinar el valor de la ordenada en el origen, $k$, debemos tener en cuenta que el valor de dicha función lineal afín en $x=a=-2$ ha de coincidir con el valor de la función $f(x)$ en $x=a=-2$. Es decir, $$-2\cdot (-2)+k=f(-2)$$ y como $f(-2)=(-2)^2+2\cdot (-2)=4-4=0$, tenemos que $$-2\cdot (-2)+k=0 \Leftrightarrow k=-4$$ Así que
$$\text{r.t.}_1:y=-2x-4$$

Caso II:
La pendiente de la recta tangente en un punto $x=a$ situado a la izquierda de $3/2$ ( esto es, del intervalor $I_2$ ) ha de ser igual a $-2$ (enunciado ), y dicho valor corresponde a la derivada de la función en dicho punto, $f'(a)$. Como para $x \succ 3/2$, $f'(x)=-2x+3$, tenemos que $(-2x+3)_{x=a}=-2$ y por tanto $$-2a+3=-2$$ de donde deducimos que $a=5/2$

Procedemos a escribir la ecuación de la recta tangente a la gráfica de la función en dicho punto $a=5/2$, que designaremos por $\text{r.t.}_2$. Repetimos los mismos pasos que en el caso I. Sabemos que la ecuación de dicha recta es de la forma $y=mx+k$, y como la pendiente de dicha recta es $m=-2$, nos queda $y=-2x+k$. Para determinar el valor de la ordenada en el origen, $k$, debemos tener en cuenta que el valor de dicha función lineal afín en $x=a=5/2$ ha de coincidir con el valor de la función $f(x)$ en $x=a=5/2$. Es decir, $$-2\cdot \dfrac{5}{2}+k=f(5/2)$$ y como $f(5/2)=-(5/2)^2+3\cdot (5/2)=5/4$, tenemos que $$-2\cdot (5/2)+k=5/4 \Leftrightarrow k=25/4$$ Así que
$$\text{r.t.}_2:y=-2x+\dfrac{25}{4}$$
$\square$

Se considera el sistema de ecuaciones (...)

ENUNCIADO. Se considera el sistema de ecuaciones dependientes del parámetro real $a$ $$\left\{\begin{matrix}(a-1)x&+&y&+&z&=&1 \\ x&+&(a-1)y&+&(a-1)z&=&1 \\ x&&&+&az&=&1 \end{matrix}\right.$$
a) Discútase el sistema según los valores de $a$
b) Resuélvase el sistema para $a=3$

SOLUCIÓN.
a)
Reduciendo el sistema por Gauss,
$\left\{\begin{matrix}(a-1)x&+&y&+&z&=&1 \\ x&+&(a-1)y&+&(a-1)z&=&1 \\ x&&&+&az&=&1 \end{matrix}\right.$

$\sim \left\{\begin{matrix}y&+&(a-1)x&+&z&=&1 \\ (a-1)y&+&x&+&(a-1)z&=&1 \\ &&x&+&az&=&1 \end{matrix}\right. \overset{-(a-1)e_1+e_2\rightarrow e_2}{\sim}$

$\sim \left\{\begin{matrix}y&+&(a-1)x&+&z&=&1 \\ &&a(a-2)x&&&=&(a-2) \\ &&x&+&az&=&1 \end{matrix}\right.$

$\sim \left\{\begin{matrix}y&+&(a-1)x&+&z&=&1 \\ &&x&+&az&=&1 \\ &&a(a-2)x&&&=&(a-2) \end{matrix}\right.$

$\sim \left\{\begin{matrix}y&+&z&+&(a-1)x&=&1 \\ &&az&+&x&=&1 \\ &&&&a(a-2)x&=&(a-2) \end{matrix}\right.$

Debemos distinguir ahora los siguientes casos:

Caso 1. Si $a=0$, la tercera ecuación conduce a una contradicción, $0=-2$, con lo cual el sistema es incompatible para este valor del parámetro.

Caso 2. Si $a=2$, la tercera ecuación es trivial, pues obtenemos $0=0$, luego el sistema tiene dos ecuaciones independientes, con lo cual el rango del mismo es $r=2$; y como el número de incógnitas es $n=3$, el sistema es compatible indeterminado con $n-r=3-2=1$ variable secundaria ( y $2$ variables principales ), según el teorema de Rouché-Fröbenius.

Caso 3. Si $a \notin \{0,2\}$, el sistema es compatible determinado, ya que $r=n=3$ ( por el teorema de Rouché-Fröbenius )

b)
Si $a=3$, como $3 \notin \{0,2\}$, estamos en el caso 3 y el sistema es compatible determinado. El sistema equivalente reducido es
$ \left\{\begin{matrix}y&+&z&+&2x&=&1 \\ &&3z&+&x&=&1 \\ &&&&3x&=&1 \end{matrix}\right.$
Despejando $x$ de la tercera ecuación, obtenemos $$x=1/3$$ sustituyendo este valor en la segunda ecuación y despejando $z$ obtenemos, $$z=2/9$$ y sustituyendo los dos valores encontrados para $x$ y $z$ en la primera ecuación y despejando $y$, se llega a $$y=1/9$$
$\square$

El tiempo, en minutos, que los empleados de unos grandes almacenes tardan en (...)

ENUNCIADO. El tiempo, en minutos, que los empleados de unos grandes almacenes tardan en llegar a su casa se puede aproximar por una variable aleatoria con distribución normal, de media $\mu$ desconocida y desviación típica/estándar $\sigma=5$ minutos. Se pide:

a) Se toma una muestra aleatoria simple de $64$ empleados y su media muestral resulta ser $\bar{x}=30$ minutos. Determínese un intervalo de confianza al $95\,\%$ para $\mu$

b) ¿ Qué tamaño mínimo debe tener una muestra aleatoria simple para que el correspondiente intervalo de confianza para $\mu$, al $99\,\%$, tenga una amplitud a lo sumo de $1$ minuto ?

SOLUCIÓN.
a)
Denotemos por $X$ a la variable aleatoria de la población "tiempo en llegar a casa". Sabemos que $X \sim N(\mu\,,\,5)$, entonces un intervalo de confianza para la estimación de la media de la población $\mu$ es $(\bar{x}-E\,,\,\bar{x}+E)$, donde $\bar{x}=30$ minutos y $E$ es el máximo error cometido en la estimación, que viene dado por $E=z_{\alpha/2}\cdot \dfrac{\sigma}{\sqrt{n}}$ y cuyo valor vamos a calcular a continuación: como el nivel de confianza es $1-\alpha=0'95$, $\alpha=0'05$ y por tanto $\alpha/2=0'025$; entonces $P\{Z \le z_{\alpha/2}\}=1-0'025=0'975$, por lo que consultando en las tablas de la distribución de probabilidad $N(0\,,\,1)$ encontramos el siguiente valor de la abscisa $z_{\alpha/2}=1'96$

Así, $E=1'96 \cdot \dfrac{5}{\sqrt{64}}=1'225$. Y, por consiguiente, el intervalo de confianza pedido para la media de la población es $(30-1'225\,,\,30+1'225)$ esto es $(28'775\,,\,31'225)$, intervalo que, en buena lógica, podemos aproximar a $(28\;,\;32)$ minutos.

b)
El intervalo de confianza de la media poblacional $\mu$, es $(\bar{x}-E\,,\,\bar{x}+E)$. Y la amplitud de dicho intervalo viene dada por $E=z_{\alpha/2}\cdot \dfrac{\sigma}{\sqrt{n}}$. Como, en este caso, $\sigma=5$ minutos, y $E \le 1$ minuto, entonces $z_{\alpha/2}\cdot \dfrac{5}{\sqrt{n}} \le 1$

Por otra parte, si $1-\alpha=0'99$, entonces $\alpha=0'01$, luego $\displaystyle P\{Z \le z_{\alpha/2}\}=1-z_{\alpha/2}$. En nuestro caso, $P\{Z \le z_{0'01/2}\}=1-0'005=0'995$, por lo que, consultando las tablas de la función de distribución de la variable aleatoria normal tipificada $Z \sim N(0,1)$, encontramos $z_{\alpha/2}=z_{0'01/2} \overset{\text{tablas}}{\approx} 2'58$

Podemos escribir ahora que $2'58\cdot \dfrac{5}{\sqrt{n}} \le 1$, así que elevando al cuadrado ambos miembros de la desigualdad resulta $n \ge \big( \dfrac{2'58 \cdot 5)}{1}\big)^2 \approx 167$ ( aproximando por exceso ), luego el tamaño mínimo de la muestra es $n_{\text{mín}} = 167$

$\square$

Sean dos sucesos aleatorios (...)

ENUNCIADO. Sean $A$ y $B$ dos sucesos de un experimento aleatorio tales que $P(A)=3/4$, $P(A|B)=3/4$ y $P(B|A)=1/4$
a) Demuéstrese que $A$ y $B$ son sucesos independientes pero no incompatibles
b) Calcúlese $P(\bar{A}|\bar{B})$
NOTA: $\bar{S}$ denota el suceso complementario/contrario del suceso $S$

SOLUCIÓN.
a)
Los sucesos $A$ y $B$ son compatibles:
Para demostrar que $A$ y $B$ son compatibles debemos probar que $P(A \cup B) \neq P(A)+P(B)$; en otras palabras, y teniendo en cuenta la propiedad general $P(A \cup B)=P(A)+P(B)-P(A \cap B)$, es necesario probar que $P(A \cap B) \neq 0$. Para ello consideremos las siguientes expresiones que vienen de la definición de probabilidad condicionada: $$P(A|B)\overset{\text{def}}{=}\dfrac{P(A \cap B}{P(B)} \quad \quad (1)$$ y $$P(B|A)\overset{\text{def}}{=}\dfrac{P(B \cap A}{P(A)}=\dfrac{P(A \cap B}{P(A)} \quad \quad (2)$$ Dividiendo, miembro a miembro, (1) entre (2), obtenemos $$\dfrac{P(A|B)}{P(B|A)}=\dfrac{P(A)}{P(B)}$$ de donde se deduce que $$P(B)=\dfrac{P(A)P(B|A)}{P(A|B)}=\dfrac{(3/4)\cdot (1/4)}{1/4}=1/4$$ Entonces $$P(A \cap B)\overset{\text(1)}{=}P(A|B)P(B)=\dfrac{3}{4}\cdot \dfrac{1}{4}=\dfrac{3}{16} \neq 0$$
$\square$

Los sucesos $A$ y $B$ son independientes:
De la definición de independencia de sucesos sabemos que $A$ y $B$ son independientes si y sólo si se cumplen las siguientes condiciones: $P(A|B)=P(A)$ y $P(B|A)=P(B)$. En efecto, con los datos del problema y los resultados obtenidos se comprueba que $P(A|B)=P(A)=\dfrac{3}{4}$ y $P(B|A)=P(B)=\dfrac{1}{4}$

Otra forma de demostrarlo es la siguiente. Los sucesos $A$ y $B$ son independientes si se cumple la siguiente igualdad $P(A \cap B)=P(A)P(B)$ ( consecuencia de la definición de sucesos independientes ). Bastará pues comprobar que, con los datos del problema y los resultados que acabamos de obtener, ésto se cumple. En efecto, hemos calculado el valor del primer miembro de la igualdad en la primera parte: $P(A \cap B)=\dfrac{3}{16}$; y, también, se ha calculado $P(B)$ que es $\dfrac{1}{4}$. Entonces, como sabemos ( enunciado ) que $P(A)=\dfrac{3}{4}$, se cumple que $P(A)P(B)=\dfrac{3}{4}\cdot \dfrac{1}{4}=\dfrac{3}{16}$

b)
Sabemos que $$P(\bar{A}|\bar{B})\overset{\text{def. cond.}}{=}\dfrac{P(\bar{A}\cap \bar{B})}{P(\bar{B})}$$ Ahora bien, de la primera ley de Morgan, $
\bar{A}\cap \bar{B}=\overline{A \cup B}$, por tanto $$P(\bar{A}|\bar{B})=\dfrac{P(\overline{A \cup B})}{P(\bar{B})}=\dfrac{1-P(A\cup B)}{1-P(B)} \quad \quad (3)$$ y, por la fórmula de inclusión-exclusión $$P(A \cup B)=P(A)+P(B)-P(A\cap B)$$ Con los datos del problema encontramos: $$P(A \cup B)=1-\dfrac{3}{4}-\dfrac{1}{4}+\dfrac{3}{16}=\dfrac{3}{16}$$ y $$1-P(B)=1-\dfrac{1}{4}=\dfrac{3}{4}$$ Y sustituyendo estos resultados en (3), obtenemos $$P(\bar{A}|\bar{B})=\dfrac{3/16}{3/4}=\dfrac{1}{4}$$
$\square$

Dada la función real de variable real (...)

ENUNCIADO. Dada la función real de variable real definida por $$f(x)=\left\{\begin{matrix}x^2+1 & \text{si} & x < 1 \\ \\ \dfrac{ax+b}{x} & \text{si} & 1 \le x \le 2 \\ \\ \sqrt{x^3+1} & \text{si} & x > 2\end{matrix}\right.$$
a) Determínense los valores que deben tomar los parámetros $a$ y $b$ para que $f(x)$ sea continua en $x=1$ y $x=2$
b) Calcúlese, para $a=4$ y $b=-2$, el área del recinto acotado por la gráfica de $f(x)$, el eje de abscisas y las rectas $x=1$ y $x=2$

SOLUCIÓN.
a)
Para que $f(x)$ sea continua en $x=1$ ha de cumplirse $$\{x^2+1:x=1\}=\{\dfrac{ax+b}{x}:x=1\}$$ y por tanto $$a+b=2 \quad \quad \quad (1)$$

Para que $f(x)$ sea continua en $x=2$ ha de cumplirse $$\{\sqrt{x^3+1}:x=2\}=\{\dfrac{ax+b}{x}:x=2\}$$ y por tanto $$2a+b=6 \quad \quad \quad (2)$$
Resolviendo ahora el sistema de ecuaciones que forman (1) y (2) $$\left\{\begin{matrix}a&+&b&=&2 \\ 2a&+&b&=&6\end{matrix}\right. \overset{e_2-e_1 \rightarrow e_2}{\sim} \left\{\begin{matrix}a&+&b&=&2 \\ a&&&=&4\end{matrix}\right. \sim \left\{\begin{matrix}&&b&=&-2 \\ a&&&=&4\end{matrix}\right. $$

b)
$$\displaystyle \text{Área}=\left|\int_{1}^{2}\,\dfrac{4x-2}{x}\,dx\right|$$ Teniendo en cuenta que una primitiva, $F(x)$, de la función $\dfrac{4x-2}{x}$ es $\displaystyle \int \dfrac{4x-2}{x} dx = 4\int dx -2 \int \dfrac{1}{x}dx = 4x-2\,\ln x$, podemos escribir $$\displaystyle \text{Área}\overset{\text{Barrow}}{=}\left|F(2)-F(1)\right|=(4\cdot 2 - 2\,\ln 2)-(4\cdot 1 - 2 \ln 1)=4-2\ln2=2\,(2-\ln2)$$

$\square$

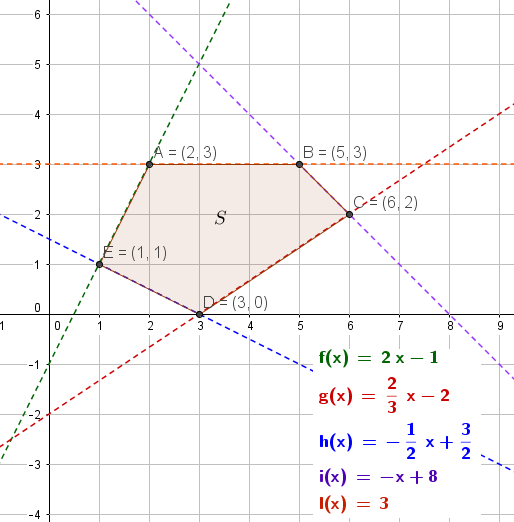
Sea la región del plano dada por el sistema de desigualdades (...)

ENUNCIADO. Sea $S$ la región del plano definida por $$\left\{\begin{matrix}2x&-&y&\ge&1 \\ 2x&-&3y&\le&6 \\ x&+&2y&\ge&3 \\ x&+&y&\le&8 \\ &&y&\le&3\end{matrix}\right.$$
a) Represéntese la region $S$ y calcúlense las coordenadas de sus vértices
b) Obténganse los valores máximo y mínimo de la función $f(x,y)=2x+y$ en la región $S$, indicando los puntos en los cuales se alcanzan dichos valores máximo y mínimo.

SOLUCIÓN.

a)
Podemos expresar la desigualdades de la siguiente forma $$\left\{\begin{matrix} y \le 2x-1 \\ y \ge \dfrac{2}{3}x-2 \\ y \ge -\dfrac{1}{2}x+\dfrac{3}{2}\\ y \le -x+8 \\ y \le 3\end{matrix}\right.$$ que es más conveniente para encontrar la región $S$ ( convexa ) del plano.

Las ecuaciones de las rectas que contienen los lados de dicha región son $$\left\{\begin{matrix} y = 2x-1 \\ y = \dfrac{2}{3}x-2 \\ y = -\dfrac{1}{2}x+\dfrac{3}{2}\\ y = -x+8 \\ y = 3\end{matrix}\right.$$

Representando dichas rectas en el plano y calculando los puntos de intersección de las mismas ( vértices de la región convexa $S$ ) obtenemos

b)
Despejando la variable dependiente $y$ de $f(x,y)\equiv k=2x+y$ se obtiene $y=-2x+k$, que representa una recta del haz de rectas paralelas de la función objetivo. El valor máximo ( respectivamente, mínimo ) de la ordenada en el origen $k$ es pues el valor máximo ( respectivamente, mínimo ) de $f$. Tal como se muestra en las siguientes figuras, hemos encontrado que el máximo corresponde a la recta del haz que pasa por $C(6,2)$, que es igual a $f(6,2)=14$; y, el mínimo, a la recta del haz que pasa por $E(1,1)$, y su valor es $f(1,1)=3$

$\square$

Se considera la matriz (...)

ENUNCIADO. Se considera la matriz $$A=\begin{pmatrix}k & -1 & 0 \\ -7 & k & k \\ -1 & -1 & k \end{pmatrix}$$
a) Estúdiese para qué valores del parámetro real $k$ la matriz $A$ tiene inversa
b) Determínese, para $k=1$, la matriz $X$ tal que $XA=\text{Id}$
NOTA: $\text{Id}$ denota la matriz identidad de tamaño $3 \times 3 $

SOLUCIÓN.
a)
$A$ tiene inversa si y sólo si $\text{det}(A)\neq 0$. Entonces, $$\begin{vmatrix}k & -1 & 0 \\ 7 & k & k \\ -1 & -1 & k \end{vmatrix}\overset{[1]}{=}(-1)\cdot \begin{vmatrix}-1 & 0 \\ k & k \end{vmatrix}-(-1)\cdot \begin{vmatrix}k & 0 \\ 7 & k \end{vmatrix}=k^2+k=0 \Leftrightarrow k \in \{-1,0\}$$ luego $A$ tiene inversa si y sólo si $k \notin \{-1,0\}$

[1] Desarrollando por los adjuntos de la tercera fila

b)
Como $k=1 \notin \{-1,0\}$, podemos afirmar que $A=\begin{pmatrix}1 & -1 & 0 \\ -7 & 1 & 1 \\ -1 & -1 & 1 \end{pmatrix}$ tiene inversa. Entonces, si $XA=\text{Id}$, $A=X^{-1}$. Procedemos a calcular la matriz inversa de $A$ por el método de reducción de Gauss-Jordan, que es muy eficiente. Se trata de transformar $(A|\text{Id})$ en $(\text{Id}|A^{-1})$, mediante operaciones elementales entre filas.

$\left(\begin{array}{ccc|ccc} 1 & -1 & 0 & 1 & 0 & 0 \\ -7 & 1 & 1 & 0 & 1 & 0 \\ -1 & -1 & 1 & 0 & 0 & 1 \end{array}\right) \overset{f_1+f_3 \rightarrow f_3; 7f_1+f_2 \rightarrow f_2}{\rightarrow} \left(\begin{array}{ccc|ccc} 1 & -1 & 0 & 1 & 0 & 0 \\ 0 & -6 & 1 & 7 & 1 & 0 \\ 0 & -2 & 1 & 1 & 0 & 1 \end{array}\right) \rightarrow$

$\overset{(-1/3)f_2+f_3 \rightarrow f_3}{\rightarrow} \left(\begin{array}{ccc|ccc} 1 & -1 & 0 & 1 & 0 & 0 \\ 0 & -6 & 1 & 7 & 1 & 0 \\ 0 & 0 & 2/3 & -4/3 & -1/3 & 1 \end{array}\right) \rightarrow$

$\overset{(-3/2)f_3+f_2 \rightarrow f_2}{\rightarrow} \left(\begin{array}{ccc|ccc} 1 & -1 & 0 & 1 & 0 & 0 \\ 0 & -6 & 0 & 9 & 3/2 & -3/2 \\ 0 & 0 & 2/3 & -4/3 & -1/3 & 1 \end{array}\right) \rightarrow$

$\overset{(-1/6)f_2+f_1 \rightarrow f_1}{\rightarrow} \left(\begin{array}{ccc|ccc} 1 & 0 & 0 & -1/2 & -1/4 & 1/4 \\ 0 & -6 & 0 & 9 & 3/2 & -3/2 \\ 0 & 0 & 2/3 & -4/3 & -1/3 & 1 \end{array}\right) \rightarrow$

$\overset{(-1/6)f_2\rightarrow f_2;(3/2)f_3 \rightarrow f_3}{\rightarrow} \left(\begin{array}{ccc|ccc} 1 & 0 & 0 & -1/2 & -1/4 & 1/4 \\ 0 & 1 & 0 & -3/2 & -1/4 & -1/4 \\ 0 & 0 & 1 & -2 & -1/2 & 3/2 \end{array}\right)$

Por consiguiente $$A^{-1}=\left(\begin{array}{ccc} -1/2 & -1/4 & 1/4 \\ -3/2 & -1/4 & -1/4 \\ -2 & -1/2 & 3/2 \end{array}\right)$$
$\square$

Ejercicios resueltos y comentados del examen extraordinario de Septiembre de 2.º de Bachillerato, realizado el 1/09/2016

[ 1 | 2 | 3 | 4 | 5 ]

Ejercicios de Matemáticas Aplicadas a las Ciencias Sociales II ( opciones A y B ), resueltos y comentados, correspondientes a las pruebas PAU de Junio de 2016, en Madrid

[ 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 ]

Cálculos con intervalos de confianza

ENUNCIADO. La masa por unidad, en gramos, de la gamba roja de Palamòs, se puede aproximar por una variable aleatoria con distribución normal de media $\mu$ desconocida y desviación típica ( estándar ) $\sigma=5$ gramos.
a) Se ha tomado una muestra aleatoria simple de $25$ gambas y la media de sus masas ha sido $\bar{x}=70$ gramos. Calcúlese un intervalo de confianza al $95\,\%$ para $\mu$
b) Sabiendo que $\mu=70$ gramos, y considerando las masas de las $12$ gambas de una caja como muestra aleatoria simple, calcúlese la probabilidad de que la masa total de esas $12$ gambas sea mayor o igual que $855$ gramos.

ENUNCIADO.
a)
Sabemos que $X \sim N(\mu\,,\,5)$, entonces un intervalo de confianza para la estimación de la media de la población $\mu$ es $(\bar{x}-E\,,\,\bar{x}+E)$, donde $\bar{x}=70$ gramos y $E$ es el máximo error cometido en la estimación, que viene dado por $E=z_{\alpha/2}\cdot \dfrac{\sigma}{\sqrt{n}}$ y cuyo valor vamos a calcular a continuación: como el nivel de confianza es $1-\alpha=0{,}95$, $\alpha=0{,}05$ y por tanto $\alpha/2=0{,}025$; entonces $P\{Z \le z_{\alpha/2}\}=1-0{,}025=0{,}975$, por lo que consultando en las tablas de la distribución de probabilidad $N(0\,,\,1)$ encontramos el siguiente valor de la abscisa $z_{\alpha/2}=1{,}96$. Así, $E=1{,}96 \cdot \dfrac{5}{\sqrt{25}}=1{,}96$. Y, por consiguiente, el intervalo de confianza pedido para la media de la población es $(70-1{,}96\,,\,70+1{,}96)$ esto es $(80{,}04\,,\,71{,}96)$ que podemos aproximar a $(80\,,\,72)$ gramos.

b)
Por el teorema Central del Límite, la variable $\bar{X}=\dfrac{X_1+\ldots+X_n}{n}$ sigue una distribución $N(\mu\,,\,\sigma/\sqrt{n})$, con lo cual la variable aleatoria $Y:=X_1+\ldots+X_n$ sigue una distribución $N(n\cdot \mu\,,\,\sigma\cdot \sqrt{n}$. En el caso que nos ocupa, $n=12$, y deseamos calcular $P\{Y \ge 855\}$. Tipificando la variable $Y$ mediante la transformación $Z=\dfrac{Y-12\cdot 70}{5\,\sqrt{12}}$, donde $Z:N(0,1)$. Así,
$P\{Y \ge 855\}=P\{Z \ge \dfrac{855-840}{5\,\sqrt{12}}\}=P\{Z \ge 0{,}8660\}=$
$=1-P\{Z\le 0{,}8660\} \quad \quad (1)$
En las tablas de la distribución de probabilidad de $Z:N(0,1)$ encontramos que $F(0,86)=0,0951$ y $F(0,87)=0,8078$; no leemos exactamente $F(0,8660)$, por lo que procedemos a interpolar linealmente en el intervalo $(0,86\,,\,0,87)$ para calcular el valor aproximado de $F(0,8660)$; así, $$F(0,8660) \approx (0,8078-0,8051)\cdot \dfrac{0,8660-0,87}{0,87-0,86}+0,8078=0,8067$$
por consiguiente, el resultado de (1), aproximado con cuatro dígitos significativos, es $1-0,8067=0,1933 \approx 19\,\%$
$\square$

Trasladando una bola de una urna a otra ...

ENUNCIADO. Tenemos dos urnas A y B. La urna A contiene $5$ bolas: $3$ son rojas y $2$ son blancas. La urna B contiene $6$ bolas: $2$ rojas y $4$ blancas. Se extrae una bola al azar de la urna A y se deposita en la urna B. Seguidamente, se extrae una bola al azar de la urna B. Calcúlese la probabilidad de que:
a) La segunda bola extraída sea roja
b) Las dos bolas extraídas sean blancas

ENUNCIADO.
Denotaremos los sucesos de la siguiente manera:
$B_r$: extraer bola roja de la urna B
$B_b$: extraer bola blanca de la urna B
$A_r$: extraer bola roja de la urna A
$A_b$: extraer bola blanca de la urna A

a)
Teniendo en cuenta que $B_r=(B_r \cap A_b ) \cup ( B_r \cap A_r )$, la probabilidad de $B_r$ es $$P(B_r)=P( (B_r \cap A_b ) \cup ( B_r \cap A_r )$$ y como $(B_r \cap A_b )$ y $( B_r \cap A_r )$ son disjuntos, lo anterior queda $$P(B_r)=P(B_r \cap A_b ) +P( B_r \cap A_r )$$ y por la definición de probabilidad condicionada $$P(B_r)=P(B_r | A_b ) \cdot P(A_b) +P( B_r | A_r ) \cdot P( A_r)$$
poniendo ahora los datos del problema ( aplicamos la regla de Laplace ),
$$P(B_r)=\dfrac{2}{7} \cdot \dfrac{2}{5} + \dfrac{3}{7} \cdot \dfrac{3}{5}$$ y haciendo las operaciones $$P(B_r)=\dfrac{13}{35} \approx 37\,\%$$

b)
Por la definición de probabilidad condicionada, podemos escribir la probabilidad pedida de la forma
$$P(B_b \cap A_b)=P(B_b | A_b)\cdot P(A_b)$$
y teniendo en cuenta que $P(B_b|A_b)=1-P(\bar{B_b}|A_b)=1-P(B_r|A_b)$ lo anterior se escribe de la forma
$$P(B_b \cap A_b)=(1-P(B_r|A_b))\cdot P(A_b)$$ y poniendo los datos $$P(B_b \cap A_b)=(1-\dfrac{2}{7})\cdot \dfrac{2}{5}=\dfrac{2}{7}\approx 29\,\%$$
$\square$

Integrar y derivar ...

ENUNCIADO. Conocida la derivada de una función real de variable real es $$f'(x)=6\,x^2+4\,x-2$$ se pide:
a) Determínese la expresión de $f(x)$ sabiendo que $f(0)=5$
b) Determínense los intervalos de crecimiento y decrecimiento de la función $f$ así como sus máximos y mínimos locales, si los tuviese.

SOLUCIÓN.
a)
La función $f(x)$, en las condiciones del enunciado, viene dada por una primitiva de la función $f'(x)$. Calculando pues la integral indefinida de $f'(x)$, $$\displaystyle \int\,(6\,x^2+4x-2)\,dx=2\,x^3+2\,x^2-2\,x+C$$ Imponiendo ahora que $f(0)=5$, determinaremos el valor de la constante de integración $$5=2\cdot 0^3+2\cdot 0^2-2\cdot 0+C \Leftrightarrow C=5$$ por consiguiente la función pedida es $$f(x)=2\,x^3+2\,x^2-2\,x+5$$

b)
Veamos cuáles son los extremos relativos. La condición necesaria de existencia de los mismos es $f')0)=0$, por tanto $6\,x^2+4\,x-2=0$, esto es $$3\,x^2+2\,x-1=0 \Leftrightarrow x=\dfrac{-2\pm \sqrt{2^2-4 \cdot (-1) \cdot 3}}{2 \cdot 3}=\left\{\begin{matrix}\dfrac{1}{3} \\ \\ -1\end{matrix}\right.$$

Para averiguar qué tipo de extremos relativos son, utilizaremos el criterio del signo de la segunda derivada $f''(x)=12\,x+4$. Como $f''(-1)=-8 \prec 0$, $x_{1}^{*}=-1$ corresponde a la abscisa de un máximo local; y, al ser $f''(1/3)=8 \succ 0$, $x_{2}^{*}=\dfrac{1}{3}$ es la abscisa de un mínimo local. El valor de función para $x_{1}^{*}=-1$ es $f(-1)=7$, luego las coordenadas del máximo local son $Máx(-1\,,\,7)$; y, el valor de función para $x_{2}^{*}=1/3$ es $f(1/3)=\dfrac{125}{27}$, luego las coordenadas del mínimo local son $Mín(1/3\,,\,125/27)$

A partir de las abscisas del mínimo y del máximo local, deducimos que hay dos intervalos de crecimiento: $(-\infty\,,\,-1)$ y $(1/3\,,\,+\infty)$, y un sólo intervalo de decrecimiento: $(-1\,,\,1/3)$
$\square$

Analizar la función ...

ENUNCIADO. Se considera la función real de variable real $$f(x)=\left\{\begin{matrix}\dfrac{-x+b}{x-2}&\text{si}& x\le -1 \\ \\ \dfrac{x^2+6x+5}{x^2+4x+3}&\text{si}& x \succ -1 \end{matrix}\right.$$
a) Determínese para qué valores del parámetro $b$ la función $f(x)$ es continua en $x=-1$
b) Calcúlense las asíntotas de $f(x)$

SOLUCIÓN.
a)
Para que la función sea continua en $x=-1$ debe existir el límite $\displaystyle \lim_{x \rightarrow -1}\,f(x)$ y, para ello, han de existir los límites laterales y tener el mismo valor. Veamos cuáles son los límites laterales:
$$\displaystyle \lim_{x \rightarrow -1^{-}}\,f(x)=\dfrac{1+b}{3}$$ y $$\displaystyle \lim_{x \rightarrow -1^{+}}\,f(x)\overset{\text{ind.}}{=}\dfrac{0}{0}\overset{\text{factorizando}}{=}\lim_{x \rightarrow -1^{+}}\,\dfrac{(x+1)(x+5)}{(x+1)(x+3)}=\lim_{x \rightarrow -1^{+}}\,\dfrac{x+5}{x+3}=2$$ Imponiendo la igualdad de dichos límites laterales $$\dfrac{1+n}{3}=2 \Leftrightarrow b=5$$ Así, para $b=5$, $$\displaystyle \lim_{x \rightarrow -1^{-}}\,f(x) = \lim_{x \rightarrow -1^{+}}\,f(x) = f(-1)=2$$ y la función es continua en $x=-1$

b)
En el conjunto de valores de $x$ que toman imágenes de acuerdo con el primer tramo de función no hay ninguna asíntota vertical, ya que el denominador se anula para $x=2 \succ -1$; tampoco hay asíntontas verticales para el conjunto de valores de $x$ que toman imágenes con el segundo tramo, pues el denominador se anula para $x=-3 \prec -1$. Por consiguiente, la función $f(x)$ no tiene asíntotas verticales.

Veamos ahora si tiene asíntotas oblicuas ( incluyendo las horizontales ): $y=m\,x+k$. Para el primer tramo, $$m=\displaystyle \lim_{x\rightarrow -\infty}\,\dfrac{x-5}{x\,(x-2)}=0$$ luego al tener pendiente nula, sólo tiene una asíntota horizontal; calculemos ahora el valor de la ordenada en el origen $$k=\displaystyle \lim_{x\rightarrow -\infty}\,f(x)-m\,x=\lim_{x\rightarrow -\infty}\,\dfrac{x-5}{x-2}-0\cdot x=\lim_{x\rightarrow -\infty}\,\dfrac{x-5}{x-2}=1$$ por consiguiente encontramos la siguiente asíntota horizontal: $\text{a.h.}:y=1$. Si procedemos de la misma forma con el segundo tramo de la función, encontramos el mismo resultado. $\square$

Discusión y resolución de un sistema de ecuaciones lineales

ENUNCIADO. Se considera el sistema de ecuaciones lineales $$\left\{\begin{matrix}x&+&2\,y&+&z&=&1 \\ x&+&2\,y&+&3\,z&=&0 \\ x&+&a\,y&+&2\,z&=&0 \end{matrix}\right.$$

a) Discútase para los diferentes valores del parámetro $a \in \mathbb{R}$
b) Resuélvase para $a=0$

SOLUCIÓN.
a)
La matriz ampliada de los coeficientes del sistema es $(A|b) =\left(\begin{array}{ccc|c}
1 & 2 & 1 & 1 \\
1 & 2 & 3 & 0\\
1 & a & 2 & 0\\
\end{array}\right)$. Para realizar el estudio de rangos ( y aplicar el teorema de Rouché-Fröbenius ), procedemos a reducir la matriz por Gauss, puesto que las matrices que así se van obteniendo son equivalentes en rango a la original ( Nota: además, el proceso nos proporciona sistemas de ecuaciones equivalentes en solución al original, lo cual facilitará la resolución del segundo apartado ).

$\left(\begin{array}{ccc|c}
1 & 2 & 1 & 1 \\
1 & 2 & 3 & 0\\
1 & a & 2 & 0\\
\end{array}\right) \overset{(-1)\cdot f_1+f_2 \rightarrow f_2; (-1)\cdot f_1+f_3 \rightarrow f_3}{ \sim} \left(\begin{array}{ccc|c}
1 & 2 & 1 & 1 \\
0 & 0 & 2 & -1\\
0 & a-2 & 1 & -1\\
\end{array}\right) \sim$
$\overset{\text{intercambiando} f_2 y f_3}{\sim} \left(\begin{array}{ccc|c}
1 & 2 & 1 & 1 \\
0 & a-2 & 1 & -1\\
0 & 0 & 2 & -1\\
\end{array}\right)$ y el sistema equivalente es $$\left\{\begin{matrix}x&+&2\,y&+&z&=&1 \\ &&(a-2)\,y&+&z&=&-1 \\ &&&&2\,z&=&-1 \end{matrix}\right.$$

Observemos que:
I) Si $a-2=0 \Leftrightarrow a=2$, entonces las dos últimas ecuaciones son incompatibles, luego el sistema es incompatible.
II) Para cualquier otro valor de $a$ ( distinto de $2$ ), se tiene que $\text{rango}(A|b)=\text{rango}(A)=3$, luego el sistema es compatible; y, además, determinado, pues el valor de los rangos coincide con el del número de incógnitas.

b)
Si $a=0 \neq 2$ estamos en el segundo caso, con lo cual existe una única solución ( sistema compatible determinado ), que representa un punto en el espacio $\mathbb{R}^3$. Procedemos a resolver el sistema para dicho valor del parámetro $a$:
El sistema equivalente es $$\left\{\begin{matrix}x&+&2\,y&+&z&=&1 \\ &&-2\,y&+&z&=&-1 \\ &&&&2\,z&=&-1 \end{matrix}\right.$$

Iniciamos el proceso de sustitución retrógrada:
i) De la tercera ecuación, obtenemos $z=-1/2$

ii) Sustituyendo este valor en la segunda ecuación, podemos escribir $-2y-\dfrac{1}{2}=-1$, y, despejando $y$, se obtiene $y=1/4$

iii) Finalmente, sustituyendo los valores encontrados para $z$ y para $y$ en la primera ecuación, encontramos $x+2\cdot \dfrac{1}{4}-\dfrac{1}{2}=1$, de donde, despejando $x$, se obtiene $x=1$

Así, pues, la solución viene dada por el punto $(1\,,\,1/4\,,\,-1/2)$
$\square$

Intervalos de confianza

ENUNCIADO. La producción diaria de leche, medida en litros, de una cierta granja de ganado vacuno se puede aproximar por una variable aleatoria con distribución normal de media $\mu$ desconocida y desviación estándar $\sigma=50$ litros.
a) Determínese el tamaño mínimo de una muestra aleatoria simple para que el intervalo de confianza par $\mu$ al $95\,\%$ tenga una amplitud a lo sumo de $10$ litros
b) Se toman datos de producción de $25$ días, escogidos al azar. Calcúlese la probabilidad de que la media de las producciones obtenidas, $\bar{X}$, sea menor o igual que $940$ litros si sabemos que $\mu=950$ litros.

SOLUCIÓN.
a)
Sea $X \sim N(\mu,50)$. La amplitud del intervalo de confianza es el máximo error que se comete en la estimación de $\mu$ y viene dado por $E=z_{\alpha/2}\cdot \dfrac{\sigma}{\sqrt{n}}$. Entonces, según la información del enunciado, $E \ge 10$, por tanto $$z_{\alpha/2}\cdot \dfrac{\sigma}{\sqrt{n}} \ge 10$$

Teniendo en cuenta que el nivel de confianza de la estimación es $1-\alpha=0,95$, $\alpha=0,05$, luego $\alpha/2=0,025$; y como $P\{Z \le z_{\alpha/2}\}=1-\alpha/2=1-0.025=0,975$, consultando en las tablas de la función de distribución de probabilidad $N(0\,,\,1)$ encontramos que la abscisa $z_{\alpha/2}$ es igual a $1,96$. Así, $$1,96\cdot \dfrac{50}{\sqrt{n}} \ge 10$$ con lo cual $$n \ge \left(\dfrac{1,96 \cdot 50}{10}\right)^2$$ y simplificando encontramos que $$n \ge 96,04 \approx 97 \; \; \text{(aproximando por exceso)}$$

b)
A partir de los datos $\mu=950$ gramos, $\sigma=50$ gramos y $n=25$, debemos calcular $$P\{\bar{X} \le 940\}$$ Por el teorema Central del Límite, sabemos que $\bar{X}$ sigue una distribución $N(950,\dfrac{50}{\sqrt{25}})$, luego tipificando la variable aleatoria $\bar{X}$ mediante la transformación $Z = \dfrac{\bar{\bar{X}-\mu}}{\sigma/\sqrt{n}}$ podemos escribir
$P\{\bar{X} \le 940\}=P\{Z \le \dfrac{940-950}{50/\sqrt{25}}==P\{Z \le -1\}=$
$=P\{Z \ge 1\}$, por la simetría de la función de densidad con respecto al eje de ordenadas
$=1-P\{Z\le 1\}$, por la propiedad del contrario
$=1-F(1)$
$=1-0{,}8413$, consultando las tablas de la función de distribución de probabilidad $F(z)$, siendo $Z:N(0\,,\,1)$
$=0{,}1587 \approx 16\,\%$

$\square$

Cálculo de probabilidades con sucesos condicionados

ENUNCIADO. Una conocida orquesta sinfónica está compuesta por un $55\,\%$ de varones y un $45\,\%$ de mujeres. En la orquesta un $30\,\%$ de los instrumentos son de cuerda. Un $25\,\%$ de las mujeres de la orquesta interpreta un instrumento de cuerda. Calcúlese la probabilidad de que un intérprete de dicha orquesta elegido al azar:
a) Sea una mujer si se sabe que es intérprete de un instrumento de cuerda
b) Sea intérprete de un instrumento de cuerda y sea varón

SOLUCIÓN.
Denotemos por $V$ al suceso "elegir un intérprete que sea varón"; por $M$ al suceso "elegir un intérprete que sea mujer", y por $C$ al suceso "elegir un intérprete de cuerda".

a)

Como $M \cap C = C \cap M$, podemos escribir $P(M \cap C)=P( C \cap M)$, y, por la definición de probabilidad condicionada, $$P(M|C)\,P(C)=P(C|M)\,P(M)$$ con lo cual $$P(M|C)=\dfrac{P(C|M)\,P(M)}{P(C)}$$ poniendo los datos: $$P(M|C)=\dfrac{0{,}25\cdot 0{,}45}{0{,}3}=0{,}375$$

b)

$P(C \cap V)=P(V \cap C)\overset{\text{p. cond.}}{=}(P(V|C)\,P(C)\overset{\text{prop. del contrario}}{=}(1-P(\bar{V}|C))\,P(C)=$

$=(1-P(M|C))\,P(C)=(1-0{,}375)\cdot 0{,}3 = 0{,}1875$

$\square$

Un ejercicio de derivación e integración

ENUNCIADO. Se considera la función real de variable real $f(x)=x^3+8$. Se pide:
a) Determínese el área de la región acotada delimitada por la gráfica de $f(x)$, el eje de abscisas y por las rectas $x=-3$ y $x=-1$
b) Calcúlese la ecuación de la recta tangente a la gráfica de la función en el punto de abscisa $x=1$

SOLUCIÓN.
a)
El área pedida es igual $\displaystyle \left|\int_{-3}^{-1}\,(x^3+8)\,dx \right|$. Calculando la integral indefinida ( primer teorema fundamental del cálculo ): $\displaystyle \int_{-3}^{-1}\,(x^3+8)\,dx$, vemos que una función primitiva de la función del integrando es $\dfrac{1}{4}\,x^4+8,x$, luego por la regla de Barrow ( segundo teorema fundamental del cálculo ), $$\displaystyle \int_{-3}^{-1}\,(x^3+8)\,dx=$$ $$=\left[ \dfrac{1}{4}\,x^4+8,x \right]_{-3}^{-1}=\left( \dfrac{1}{4}\cdot (-1)^4+8\cdot (-1)\right)-\left(\dfrac{1}{4}\cdot (-3)^4+8\cdot (-3)\right)=-4$$ y sacando el valor absoluto obtenemos que el área pedida es igual a $4$ unidades arbitrarias de área.

b)
La ecuación de la recta tangente en el punto $P$ de abscisa $x=1$ viene dada por $\text{r.t.}_{P}:y=m\,x+k$.

i) Calculamos, primero, la pendiente de la recta en el punto pedido: $$m\overset{\text{def}}{=}f'(x_P)=f'(1)=\left(3\,x^2\right)_{x=1}=3$$

ii) Calculamos ahora el valor de la ordenada en el origen, $k$, de la recta tangente. Como la ordenada de la recta en el punto de tangencia es igual al valor de función en dicho punto podemos escribir que $3\cdot 1+k=f(1)$, esto es, $3+k=1^3+8$ y por tanto $3+k=9$, con lo cual $k=6$.

Así, la ecuación pedida es $\text{r.t.}_{P}:y=3\,x+6$

$\square$

Un ejercicio de programación lineal

ENUNCIADO. Sea $\mathcal{R}$ la región del plano definida por: $$\left\{\begin{matrix}x&+&y&\le&5\\ -x&+&y&\le&3\\ \dfrac{1}{2}\,x&-&y&\le&-2 \end{matrix}\right.$$
Se pide:
a) Representar la región $\mathcal{R}$ y calcular las coordenadas de sus vértices
b) Obténganse los valores máximo y mínimo de la función $f(x,y)=2\,x+y$ en la región $\mathcal{R}$, indicando los puntos de $\mathcal{R}$ en los que se alcanzan dichos valores máximo y mínimo.

SOLUCIÓN.

a)
Región factible:

$\mathcal{R}:\left\{\begin{matrix} y+x\le 5 \\ y-x \le 3 \\ \dfrac{1}{2}\,x-y \le -2\end{matrix}\right. \sim \left\{\begin{matrix} y \le -x+5\\ y \le x+3 \\ y \ge \dfrac{1}{2}\,x+2 \end{matrix}\right. \quad \quad (1)$
Las rectas delimitadoras de la región factible son, por tanto, $\left\{\begin{matrix} r:y=-x+5\\ s:y=x+3\\ t:y=\dfrac{1}{2}\,x+2\end{matrix}\right.$ Analizando el sentido de las desigualdades de (1) obtenemos el triángulo de la figura como polígono ( convexo ) que corresponde a la región factible. Vamos ahora a calcular las coordenadas de los vértices $A,B$ y $C$.

$A=s \cap t$ luego $A: \left\{\begin{matrix} y=x+3 \\ y=\dfrac{1}{2}\,x+2\end{matrix}\right.$ que tiene como solución el punto de coordenadas $(1,2)$
$B=r \cap t$ luego $B: \left\{\begin{matrix} y=-x+5 \\ y=\dfrac{1}{2}\,x+2\end{matrix}\right.$ que tiene como solución el punto de coordenadas $(2,3)$
$C=s \cap r$ luego $C: \left\{\begin{matrix} y=x+3 \\ y=-x+5\end{matrix}\right.$ que tiene como solución el punto de coordenadas $(1,4)$

b)
La región factible ( convexa ) es, en este caso, acotada superior e inferiormente, por lo que podemos asegurar que existe máximo y que existe mínimo. Veamos cuáles son y para qué puntos de la región factible se dan.

La función objetivo $f(x,y)=2x+y$ podemos expresarla de la forma $y=-2x+k$, donde la ordenada en el origen $k$ representa los valores $k\equiv f(x,y)$ de cada una de las rectas del haz de rectas paralelas ( familia de rectas de la función objetivo ). Así, los puntos de la región factible que estén sobre la recta ( o las rectas ) que tengan un valor de $k$ máximo ( respectivamente, mínimo ) corresponden a los puntos donde la función alcanza el máximo ( respectivamente, el mínimo ).

Tal como se puede apreciar en la figura, el máximo de la función objetivo $f(x,y)$ se alcanza en el punto $B(2,3)$ y por tanto su valor es igual a $f(2,3)=2\cdot 2+3=7$; y el mínimo de $f(x,y)$ se alcanza en el punto $A(-2,1)$ y su valor es igual a $f(-2,1)=2\cdot (-2)+1=-3$

$\square$

Cálculo con matrices

ENUNCIADO. Considérense las matrices
$A=\begin{pmatrix} 3 & 2 & 2 \\ 1 & 7 & 4 \\ 4 & 5 & 2 \end{pmatrix}$   $B=\begin{pmatrix} 2 & 1 \\ 5 & 3 \\ 0 & 1 \end{pmatrix}$   $C=\begin{pmatrix} 2 & 4 & 8 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{pmatrix}$
a) Calcular el producto de matrices   $A\,C\,C^{\top}\,A^{-1}$
b) Calcular la matriz $M=A\,B$. ¿ Existe $M^{-1}$

SOLUCIÓN.
a)
$A\,C\,C^{\top}\,A^{-1}=((A\,C)\,C^{\top})\,A^{-1} \quad \quad (1)$ ( por la propiedad asociativa del producto de matrices )
Entonces,
$A\,C=\begin{pmatrix} 3 & 2 & 2 \\ 1 & 7 & 4 \\ 4 & 5 & 2 \end{pmatrix} \, \begin{pmatrix} 2 & 4 & 8 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 6 & 14 & 28 \\ 2 & 11 & 19 \\ 8 & 21 & 39 \end{pmatrix}$
Teniendo en cuenta que la matriz traspuesta de $C$ es $C^{\top}=\begin{pmatrix} 2 & 0 & 0 \\ 4 & 1 & 0 \\ 8 & 1 & 1 \end{pmatrix}$, tenemos que $(A\,C)\,C^{\top}=\begin{pmatrix} 6 & 14 & 28 \\ 2 & 11 & 19 \\ 8 & 21 & 39 \end{pmatrix} \, \begin{pmatrix} 2 & 0 & 0 \\ 4 & 1 & 0 \\ 8 & 1 & 1 \end{pmatrix} = \begin{pmatrix} 292 & 42 & 28 \\ 200 & 30 & 19 \\ 412 & 60 & 39 \end{pmatrix}$

Procedemos ahora a calcular la matriz inversa de $A$; para ello se aconseja emplear el método de Gauss-Jordan ( si bien también podemos emplear el método de la matriz adjunta ). Recordemos que el método de Gauss-Jordan consiste en realizar operaciones elementales de reducción al objeto de transformar $(A|I)$ en $(I|A)$. Omitimos los cálculos, pues ya los hemos explicado en muchas ocasiones ( por ejemplo en este otro ejercicio ), y damos directamente el resultado: $$A^{-1}=\begin{pmatrix} 1/6 & -1/6 & 1/6 \\ -7/18 & 1/18 & 15/18 \\ 23/36 & 7/36 & -19/36 \end{pmatrix}$$

Y, finalmente, ya podemos completar el cálculo (1),
$((A\,C)\,C^{\top})\,A^{-1}=\begin{pmatrix} 292 & 42 & 28 \\ 200 & 30 & 19 \\ 412 & 60 & 39 \end{pmatrix} \, \begin{pmatrix} 1/6 & -1/6 & 1/6 \\ -7/18 & 1/18 & 15/18 \\ 23/36 & 7/36 & -19/36 \end{pmatrix} =$
$$=\begin{pmatrix} 51 & -368/9 & 410/9 \\ 1217/36 & -1007/36 & 1139/36 \\ 281/4 & -231/4 & 259/4 \end{pmatrix}$$

b)
Antes de empezar el cálculo, notemos que el producto de matrices $A_{3\times 3}\,B_{3 \times 2}$, por lo que la matriz que resulta de ello, $M$, ha de ser de tamaño $3 \times 2$. Procedemos al cálculo: $$M=\begin{pmatrix} 3 & 2 & 2 \\ 1 & 7 & 4 \\ 4 & 5 & 2 \end{pmatrix} \, \begin{pmatrix} 2 & 1 \\ 5 & 3 \\ 0 & 1 \end{pmatrix}=\begin{pmatrix} 16 & 11 \\ 37 & 26 \\ 33 & 21 \end{pmatrix}$$

En respuesta a la segunda pregunta de este apartado: la matriz $M$ no es cuadrada, luego no está definida la matriz inversa para $M$.

$\square$

Ejercicios resueltos y comentados del examen global de 2.º de Bachillerato, realizado el Viernes 13/05/2016

[ 1 | 2 | 3 | 4 | 5 ]

Estimación de la media de la población por intervalo de confianza

ENUNCIADO. Se sabe que la variable aleatoria asociada a una cierta característica de una población sigue una distribución $N(\mu\,,\,2{'}51)$. Se ha extraído ( de la población ) una muestra aleatoria simple, al objeto de realizar una estimación por intervalo ( de confianza ) de la media de la población $\mu$, al $95\,\%$ de confianza. El intervalo de confianza de $\mu$ ha resultado ser $$\text{IC}=(5{'}34\,,\,5{'}86)$$ Se pide:
a) El valor de $\bar{x}$ ( media medida en la muestra )
b) El máximo error, $E$, que se comete en la estimación de $\mu$
c) El tamaño, $n$, de la muestra

SOLUCIÓN.
a) La media medida en la muestra es igual al centro del intervalo de confianza, luego $$\bar{x}=\dfrac{5{'}34+5{'}86}{2}=5{'}6$$
b) El máximo error en la estimación es la amplitud del intervalo de confianza, por tanto $$E=\dfrac{5{'}86-5{'}34}{2}=0{'}26$$
c) Despejando $n$ la fórmula del error, $E=z_{\alpha/2}\cdot \dfrac{\sigma}{\sqrt{n}}$, obtenemos $$n=\left(\dfrac{z_{\alpha/2}\cdot \sigma}{E}\right)^2 \quad \quad (1)$$
Sólo nos falta determinar el valor de la abscisa $z_{\alpha/2}$, que despejamos de $1-\alpha=0{'}95$, obteniendo $\alpha=0{'}05$ y, por tanto, $\alpha/2=0{'}025$. Ahora, sabiendo que $F(z_{\alpha/2})\equiv P\{Z \le z_{\alpha/2}\}=1-0{'}025=0{'}975$, consultando las tablas de la función de distribución de probabilidad $F(z)$ ( siendo $Z$ una d. $N(0,1)$ ), encontramos que $z_{\alpha/2}=1{'}96$

Sustituyendo, pues, los datos en (1), obtenemos el tamaño de la muestra $n=\left( \dfrac{1{'}96 \cdot 2{'}51}{0{'}26} \right)^2 \approx 359$ ( aproximando por exceso a las unidades ). $\square$

Probabilidad condicionada

ENUNCIADO. Se nos informa de que, en una empresa, el $45\,\%$ de las personas empleadas son hombres, y el $55\,\%$ son mujeres. Se sabe, también, que, entre las personas empleadas que tienen menos de treinta años, el $60\,\%$ son hombres, y el $70\,\%$ son mujeres. Hemos elegido, al azar, una persona que está empleada en dicha empresa. Se pide:
a) Calcular la probabilidad de que la persona elegida ( al azar ) tenga menos de treinta años
b) En el supuesto de que la persona elegida ( al azar ) haya resultado tener menos de treinta años, ¿ cuál es la probabilidad de que sea una mujer ? ¿ Y de que sea un hombre ?.

SOLUCIÓN.
Llamemos $T$ al suceso "ser un trabajador menor de $30$ años"; $H$, al suceso "ser un trabajador de genero masculino"; y, $M$, al suceso "ser un trabajador de genero femenino".

a)
Como $\{M\,,\,H\}$ constituye una partición de $\Omega$, tenemos que $T=(T \cap M ) \cup (T \cap H)$, luego por el Teorema de la Probabilidad Total, $$P(T)=P(T|M)\cdot P(M) + P(T|H)\cdot P(H)$$ y teniendo en cuenta que $P(H)=0{,}55$; $P(M)=0{,}45$; $P(T|M)=0{,}7$, y $P(T|H)=0{,}6$, obtenemos: $$P(T)=0{,7}\cdot 0{,}45 + 0{,}6\cdot 0{,}55 = 0{,}645$$

b)
Por el teorema de Bayes, podemos escribir $$P(M|T)=\dfrac{P(T|M)\cdot P(M)}{P(T)}$$ y poniendo los datos, obtenemos $P(M|T)=\dfrac{0{,}7 \cdot 0{,}45}{0{,}645}\approx 0{,}488$
y, de forma similar, $$P(H|T)=\dfrac{P(T|H)\cdot P(H)}{P(T)}$$ y, con los datos, $P(H|T)=\dfrac{0{,}6 \cdot 0{,}55}{0{,}645}\approx 0{,}512$
$\square$

Ejercicio de programación lineal

ENUNCIADO. En un cierto problema de programación lineal, la función objetivo es $$f(x,y)=-3x+10\,y$$ siendo la región factible, el cuadrilátero convexo del plano cuyos vértices son $A(1,4)$, $B(2,6)$, $C(4,3)$ y $D(3,2)$ . Se pide:
a) Representar la región factible y determinar el sistema de desigualdades ( restricciones ) correspondiente
b) Representar la gráfica de una de las rectas del az de rectas paralelas asociadas a la función objetivo en el mismo diagrama que se ha representado la región factible
c) ¿ Qué punto de la región factible corresponde al máximo de la función ? ¿ Cuál es el valor de dicho máximo ?
d) ¿ Qué punto de la región factible corresponde al mínimo de la función ? ¿ Cuál es el valor de dicho mínimo ?

SOLUCIÓN.
a)

Las recta que pasa por los puntos $A(1,4)$ y $B(2,6)$ tiene por ecuación $y=2\,x+2$, y para los puntos con abscisas comprendidas entre $x_A=1$ y $x_B=2$, las correspondientes ordenadas de los puntos que quedan por debajo del segmento $AB$ han de cumplir $y \le 2x+2$

Las recta que pasa por los puntos $B(2,6)$ y $C(4,3)$ tiene por ecuación $y=-\dfrac{3}{2}\,x+9$, y para los puntos con abscisas comprendidas entre $x_B=2$ y $x_C=4$, las correspondientes ordenadas de los puntos que quedan por debajo del segmento $BC$ han de cumplir $y \le -\dfrac{3}{2}\,x+9$

Las recta que pasa por los puntos $C(4,3)$ y $D(3,2)$ tiene por ecuación $y=x-1$, y para los puntos con abscisas comprendidas entre $x_D=3$ y $x_C=4$, las correspondientes ordenadas de los puntos que quedan por encima del segmento $CD$ han de cumplir $y \ge x-1$

Las recta que pasa por los puntos $A(1,4)$ y $D(3,2)$ tiene por ecuación $y=-x+5$, y para los puntos con abscisas comprendidas entre $x_A=1$ y $x_D=3$, las correspondientes ordenadas de los puntos que quedan por debajo del segmento $AD$ han de cumplir $y \ge -x+5$

Así, el sistema de restricciones viene dado por $$\left\{\begin{matrix}y & \le & 2x&+&2 \\ y& \le &-\dfrac{3}{2}\,x&+&9\\ y &\ge &x&-&1 \\ y & \ge &-x &+& 5\end{matrix}\right.$$

b)
Sea $f(x,y):=c$; entonces, despejando $y$ de $c=-3x+10\,y$, obtenemos $y=\dfrac{3}{10}\,x+\dfrac{c}{10}$. Llamando ( por comodidad ) $k$ a $\dfrac{c}{10}$, podemos escribir la ecuación del az de rectas paralelas de la función objetivo de la forma $y=\dfrac{3}{10}\,x+k$. La recta roja discontinua ( en el gráfico ) es una de las rectas de dicho az. Dando valores arbitrarios a $k$ ( y por lo tanto a $c$, que es el valor de función ) podemos explorar la región factible para visualizar cuáles son los puntos de la misma donde se alcanza el máximo y el mínimo pedidos.

En la construcción, hecha con GeoGebra, se ha preparado una barra deslizadora para cambiar el valor de $k$ y, así, realizar el desplazamiento de dicha recta paralela a sí misma, dando lugar a las otras rectas del az. El segmento de color rojo sobre el eje de ordenadas indica el valor de $k$, que es proporcional al valor de $c$ ( esto es, de $f(x,y)$ ), observándose que el máximo de $f(x,y)$ ( proporcional al máximo de $k$ ) se obtiene en el punto $B(2,6)$; y, el mínimo en el punto $D(3,2)$

c)-d)
Evaluando la función en los cuatro vértices del cuadrilátero convexo que forma la región factible al objeto de determinar el valor del máximo ( que ya sabemos que corresponde a $B$ ) y del mínimo ( que ya sabemos que corresponde a $D$ ), obtenemos:
$$f_{\text{máx}}=f(x_B,y_B)=-3 \cdot 2 + 10 \cdot 6 = 54$$
$$f_{\text{mín}}=f(x_D,y_D)=-3 \cdot 3 + 10 \cdot 2 = 11$$

$\square$

Analizar la función, calcular la recta tangente en el punto (...), y determinar el área delimitada por (...)

ENUNCIADO. Sea la función real, de una variable real, $f(x)=x^3-4\,x$. Se pide:
a) Calcular los extremos relativos de la función y clasificarlos según su naturaleza. ¿ Cuáles son los intervalos de crecimiento/decrecimiento ? ¿ Está acotada esta función ?
b) Calcular las raíces de la función y la ordenada en el origen
c) ¿ Tiene esta función algún punto de inflexión ? En caso afirmativo, calcular sus coordenadas. Determinar los intervalos de concavidad/convexidad
d) Representar la gráfica de la función
e) Determinar la ecuación de la recta tangente a la gráfica de la función en el punto de abscisa $x=-2$
f) Calcular el área de la región del plano delimitada por la gráfica de la función y el eje de abscisas

SOLUCIÓN.
La función propuesta es un polinomio, su dominio de definición está formado por todos los números reales, y es continua y derivable en todo su dominio.
a)
Sabemos que el conjunto de extremos relativos es $\{x \in \mathbb{R}: f'(x)=0\}$. Entonces, $f'(x)=3\,x^2-4$; por tanto ( imponiendo la condición ), $$3\,x^2-4 = 0 \Leftrightarrow x_{1}^{*}=-\dfrac{2}{\sqrt{3}}\;\text{ó}\; x_{2}^{*}=-\dfrac{2}{\sqrt{3}}$$ Veamos, ahora, que tipo de extremos relativos son; para ello emplearemos el criterio del signo de la segunda derivada en dichos puntos ( pues es fácil derivar este tipo de funciones ). La función segunda derivada es $f''(x)=6\,x$. Como $f''(-2/\sqrt{3}) \prec 0$, de ello se sigue que $x_{1}^{*}=-2/\sqrt{3}$ corresponde a un máximo local, y la ordenada de dicho máximo es $f(-2/\sqrt{3})\approx 3{,}1$; por otra parte, $f''(2/\sqrt{3}) \succ 0$, por lo que $x_{2}^{*}=2/\sqrt{3}$ corresponde a un mínimo local, y la ordenada de dicho máximo es $f(2/\sqrt{3})\approx -3{,}1$

La función crece en los intervalos $(-\infty\,,\,-2/\sqrt{3})\subset \mathbb{R}$ y $(2/\sqrt{3}\,,\,+\infty)\subset \mathbb{R}$; por otra parte, decrece en el intervalo $(-2/\sqrt{3}\,,\,2/\sqrt{3})\subset \mathbb{R}$

A pesar de tener un máximo y un mínimo locales, observemos que la función no está acotada, ni inferior ni superiormente ( $\displaystyle \lim_{x\rightarrow -\infty}\,f(x)=-\infty$ y $\displaystyle \lim_{x\rightarrow +\infty}\,f(x)=+\infty$ ), por lo que no tiene máximo absoluto ni mínimo absoluto; de ello se sigue, también, que el recorrido de la función está formado por todos los números reales.

b)
El conjunto de raíces de la función viene dado por $\{x \in \mathbb{R}: f(x)=0\}$. Imponiendo la condición, $$x^3-4\,x=0 \Leftrightarrow x\,(x^2-4)=0 \Leftrightarrow x_1=0\;\text{ó}\;x_2=-2\;\text{ó}\;x_3=2$$ encontrando, pues, tres raíces.

Nota: Observemos que la función es impar, pues $f(-x)=-x^3-4\,(-x)=-x^3+4\,x=-f(x)$, y ello explica el por qué las tres raíces están igualmente espaciadas, siendo dos de ellas iguales en valor absoluto, y la tercera cero; por otra parte los puntos del plano que corresponden al máximo y el mínimo relativos son simétricos con respecto al origen de coordenadas. Esta circunstancia facilita la representación gráfica ( que realizaremos en el cuarto apartado ).

La ordenada en el origen viene dada por la imagen de $x=0$, esto es, es $f(0)=0^3-4\cdot 0=0$, lo cual indica que la gráfica de la función pasa por el origen de coordenadas.

c)
El conjunto de puntos de inflexión viene dado por $\{x \in \mathbb{R}: f''(x)=0\}$. Imponiendo la condición, $6x=0 \Leftrightarrow x=0$, luego sólo hay un punto de inflexión, que corresponde al punto $D$ del gráfico ( el origen de coordenadas ). Hay un intervalo de concavidad, que es $(-\infty\,,\,0) \subset \mathbb{R}$; y un intervalo de convexidad, que es $(0\,,\,+\infty)\subset \mathbb{R}$

d)

Los puntos $A$ y $B$ corresponden a los extremos relativos encontrados; y los puntos $C$, $D$ y $E$ a los puntos de intersección con el eje de abscisas ( $D$ también interseca al eje de ordenadas ).

e)
La recta tangente a la gráfica de la función en el punto de abscisa $0$ tiene por ecuación $y=m\,x+k$; donde $k$, aquí, es $0$, pues es evidente que pasa por el origen de coordenadas. Por otra parte $m=f'(0)=(3\,x^2-4)_{x=0}=-4$. Así, $\text{r.t. en x=0}: y=-4\,x$

f)
El área del dominio de integración ( que vemos en la figura ), por simetría, puede calcularse de la forma $$\mathcal{A}=2 \cdot \displaystyle \int_{-2}^{0}\,f(x)\,dx$$

Nota: Cuidado. El valor de la integral definida $\displaystyle \int_{-2}^{2}\,f(x)\,dx$ no da el área pedida, pues por tratarse de un dominio simétrico y ser la función impar, esta integral es nula ( la región de la derecha y la de la izquierda dan igual contribución en valor absoluto, pero una es negativa y la otra positiva ).

Calculando la integral indefinida, vemos que una primitiva de la función $f(x)=x^3-4\,x$ es $F(x)=\dfrac{1}{4}\,x^4-2\,x^2$; por lo que, aplicando la regla de Barrow, $$\displaystyle \int_{-2}^{0}\,f(x)\,dx=F(0)-F(-2)=0-(\dfrac{1}{4}(-2)^4-2\cdot (-2)^2)=4$$ por consiguiente $$\mathcal{A}=2 \cdot 4 = 8 \; \text{unidades de área}$$

$\square$

Discutir en función de los valores de un parámetro y, después, resolver el sistema para un valor dado de dicho parámetro

ENUNCIADO. Sea el siguiente sistema de ecuaciones lineales:
$$\left\{\begin{matrix}
x&+&y&-&3\,z&=&1\\
2\,x&-&y&+&a\,z&=&0\\
x&+&2\,y&+&z&=&-1\end{matrix}\right.$$
donde $a \in \mathbb{R}$ es un parámetro. \par Se pide:
a) Discutir el sistema, en función de los valores de $a$
b) Resolver el sistema para $a:=-1$

SOLUCIÓN.
a)
Intercambiamos la segunda y la tercera ecuación ( por comodidad ) y, a continuación, procedemos a reducir el sistema por el método de Gauss
$\left\{\begin{matrix}
x&+&y&-&3\,z&=&1\\
2\,x&-&y&+&a\,z&=&0\\
x&+&2\,y&+&z&=&-1\end{matrix}\right.
\sim \left\{\begin{matrix}
x&+&y&-&3\,z&=&1\\
x&+&2\,y&+&z&=&-1\\
2\,x&-&y&+&a\,z&=&0\end{matrix}\right. $
mediante las operaciones elementales entre filas $-e_1+e_2 \rightarrow e_2$ y $-2\,e_1+e_3 \rightarrow e_3$ obtenemos el siguiente sistema equivalente
$\left\{\begin{matrix}
x&+&y&-&3\,z&=&1\\
&&y&+&4\,z&=&-2\\
&&-3\,y&+&(6+a)\,z&=&-2\end{matrix}\right. $
y mediante la operación elemental entre filas $3\,e_2+e_3 \rightarrow e_3$ llegamos al sistema equivalente escalonado
$\left\{\begin{matrix}
x&+&y&-&3\,z&=&1\\
&&y&+&4\,z&=&-2\\
&&&&(18+a)\,z&=&-8\end{matrix}\right. $
Entonces, si $a=-18$, obtenemos una contradicción en la última ecuación: $0=-8$, luego para ese valor de $a$, el sistema es incompatible; y, es evidente, que para cualquier otro valor de $a$ distinto de $-18$, el sistema es compatible ( las tres ecuaciones son independientes ) y determinado ( el número de ecuaciones independientes es igual al número de incógnitas, que es $3$ ).

b)
Si $a=-1 \neq -18$, el sistema es compatible determinado ( la solución consta de un sólo valor para cada variable ). Vamos a resolverlo.
$\left\{\begin{matrix}
x&+&y&-&3\,z&=&1\\
&&y&+&4\,z&=&-2\\
&&&&17\,z&=&-8\end{matrix}\right. $
De la última ecuación, obtenemos $z=-\dfrac{8}{17}$; y, sustituyendo en la segunda ecuación y despejando $y$, llegamos a $y=-2-4\cdot (-\dfrac{8}{17})=-\dfrac{2}{17}$. Finalmente, sustituyendo estos dos valores en la primera ecuación, obtenemos $x=1-(\dfrac{-2}{17})+3\cdot ( -\dfrac{8}{17})=-\dfrac{5}{17}$
$\square$

Ejercicios ( resueltos y comentados ) del examen de los temas 13, 14 y 15, realizado el Lunes 9/05/2016

[ 1 | 2 | 3 ]

Calcular el intervalo de confianza de estimación de la media y el máximo error en la estimación

ENUNCIADO. En una muestra aleatoria simple de $200$ personas, se ha medido la aptitud para una determinada tarea, y las puntuaciones ( en una cierta escala ) tienen una
media de $33$ puntos. Sabemos, también, que la desviación típica ( de dicha característica ), en la población, es de $13$ puntos.
a) Calcular a partir de estos datos el correspondiente intervalo de confianza, a un nivel del $95\,\%$, para la estimación de la media de la población.
b) ¿ Cuál es el máximo error cometido en dicha estimación ?.

SOLUCIÓN. El estimador ( estadístico ), $\bar{X}$, de la media de la población $\mu$, sigue una distribució $N(\mu\,,\,\sigma/\sqrt{n})$ ( de acuerdo con el Teorema Central del Límite ). Así, para un nivel de confianza $1-\alpha=0{,}95$ ( y por tanto con un nivel de riesgo $\alpha=0{,}05$ ), el intervalo de confianza correspondiente a la estimación de la media de la población $\mu$ es $$\text{IC}=(\bar{x}-E\,,\,\bar{x}+E)$$ donde $E=z_{\alpha/2}\cdot \sigma/\sqrt{n}$ es el máximo error en la estimación ( la amplitud del intervalo de confianza ); $z_{\alpha/2}$ y $-z_{\alpha/2}$ son los valores de las abscisas críticas ( en el intervalo expresado en la variable tipificada $Z$ ) y que encontraremos en las tablas $N(0,1)$, y $\bar{x}$ representa el valor de la media medido en la muestra.

Calculemos el valor de la abscisa $z_{\alpha/2}$: Como $\alpha/2=0{,}05/2=0{,}025$, entonces $F(z_{\alpha/2})=P\{Z \le z_{\alpha/2}\}=1-\alpha/2=0{,975}$; y, consultando las tablas de la función de distribución de probabilidad $N(0,1)$, encontramos que $z_{\alpha/2}=1{,}96$.

a)
Así, $E=z_{\alpha/2}\cdot \sigma/\sqrt{n}=1{,}96 \cdot 13/\sqrt{200 }\approx 1{,}8$, y, por tanto, los extremos del intervalo de confianza son $33-1{,}8=31{,}2$ y $33+1{,}8)=34{,}8$, con lo cual el intervalo de confianza para la estimación de la media poblacional $\mu$ al $95\,\%$ de confianza es $\text{IC}=(31{,}2\,,\,34{,}8)$

b)
El máximo error cometido en la estimación es $E$, esto es, $1{,}8$. $\square$

Distribución de la media muestral

ENUNCIADO. La variable aleatoria $X$ de una cierta característica de una población sigue una distribución $N(10\,,\,3)$. Se toma una muestra de la población, de tamaño $50$. Se pide:
a) ¿ Qué tipo distribución corresponde al estadístico \emph{media muestral} ? ¿ Cuáles son los valores de los parámetros de la misma ?
b) ¿ Cuál es la probabilidad de que la media medida en dicha muestra, $\bar{x}$, sea mayor que $12$ ?

SOLUCIÓN.
a) Siendo la variable aleatoria $X$ ( de la población ) una distribución $N(\mu\,,\,\sigma)$, donde $\mu=10$ y $\sigma=3$, podemos afirmar que, de acuerdo con el Teorema Central del Límite, la distribución del estadístico media muestral, $\bar{X}$, es $N(\mu\,,\,\dfrac{\sigma}{\sqrt{n}})$, esto es, $N(10\,,\,\dfrac{3}{\sqrt{50}})$.

b) Así pues, $P\{X \succ 12\} \overset{\text{tipificando}}{=} P\{Z \ge \dfrac{12-10}{3/\sqrt{50}}\}\overset{\text{4 cifras decimales}}{\approx} P\{Z \ge 4,7140\}$
$=1-P\{Z \le 4,7140\}=1-F(4,7140) \overset{\text{tablas}\;N(0,1)}{\approx} 1-1 = 0$, donde $F(z)$ denota la función de distribución de probabilidad de la variable tipificada $Z$, que es $N(0,1)$
$\square$

¿ Son representativas las siguientes muestras ?

ENUNCIADO. En una facultad con $1500$ alumnos, se quiere obtener una muestra representativa para realizar una encuesta sobre la percepción que los estudiantes tienen de sí mismos acerca del compromiso personal en el seguimiento del curso. Para ello, se proponen dos maneras alternativas para seleccionar las personas que formarán la muestra: a) escoger los cien primeros alumnos que lleguen a la facultad entre las $07:50$ y las $07:55$ horas de la mañana ( la primera clase empieza a las $08:00$ horas ) ; y, b) escoger los cien primeros alumnos que hagan alguna consulta bibliográfica en la base de datos de la biblioteca de la facultad el último día laboral de la semana, durante las tres últimas horas de la jornada. ¿ Se podría aceptar que alguna de estas dos muestras es representativa ?: ¿ Sólo una de las dos ? ( y, en ese caso, ¿ cuál de ellas lo es ? ) ¿ Ninguna de las dos lo es ? ¿ Ambas los son ?.

SOLUCIÓN. Ninguna de las dos formas de muestreo propuestas dan lugar a una muestra representativa, pues se introduce sesgo en los dos casos. Este sesgo se produce por seleccionar un perfil de estudiante comprometido con su trabajo ( los muy puntuales ) o los que, aún no siéndolo necesariamente, se interesan por los recursos bibliográficos y apuran las últimas horas de la jornada semanal; es decir, por los estudiantes con una gran dedicación en la facultad. $\square$

Ejercicios resueltos y comentados del examen de los temas 10, 11 y 12 de 2.º de Bach. CCSS ( realizado el día 25/04/2016 )

[ 1 | 2 | 3 | 4 ]

Dos máquinas fabrican piezas similares ...

ENUNCIADO. Dos máquinas, $A$ y $B$, fabrican piezas similares. La producción por hora de dichas máquinas es de $300$ y $400$ piezas, respectivamente. Sabemos que el tanto por ciento de piezas defectuosas que fabrica la máquina $A$ es del $8\,\%$, y que el tanto por ciento de piezas defectuosas que fabrica la máquina $B$ es del $15\,\%$. Todas las piezas fabricadas se guardan mezcladas en el mismo almacén. Elegimos, al azar, una pieza del almacén. Se pide:
a) Calcular la probabilidad de que la pieza elegida sea defectuosa
b) Sabiendo que la pieza elegida ha resultado ser defectuosa, calcular la probabilidad de que ésta haya sido producida por la máquina $A$

SOLUCIÓN.
a)
Llamemos:
$D$ al suceso la pieza elegida es defectuosa ( de las piezas producidas por ambas máquinas )
$M_A$, elegir una pieza fabricada en la máquina $A$
$M_N$, elegir una pieza fabricada en la máquina $B$

Entonces, $\{M_A\,,\,M_B\}$ constituye un espacio completo de sucesos, esto es, $\Omega=M_A \cup M_B$, siendo $M_A \cap M_B=\emptyset$, con lo cual, $$D=(D \cap M_A) \cup (D \cap M_B)$$

Ahora bien, $(D \cap M_A) \cap (D \cap M_B) = \emptyset$, luego $(D \cap M_A)$ y $(D \cap M_B)$ son sucesos incompatibles; y, por tanto, $$P(D)=P((D \cap M_A) \cup (D \cap M_B))=P(D \cap M_A) + P(D \cap M_B)$$
Teniendo en cuenta, ahora, que
$P(D \cap M_A)=P(D|M_A)\cdot P(M_A)=\dfrac{8}{100}\cdot \dfrac{300}{700}=\dfrac{6}{175}$
y
$P(D \cap M_B)=P(D|M_B)\cdot P(M_B)=\dfrac{15}{100}\cdot \dfrac{400}{700}=\dfrac{3}{35}$
obtenemos la probabilidad total $$P(D)=\dfrac{6}{175}+\dfrac{3}{35}=\dfrac{3}{25}=12\,\%$$

b)
Por el teorema de Bayes, podemos escribir $$P(M_A|D)=\dfrac{P(D|M_A)\cdot P(M_A)}{P(D)}$$ y poniendo los datos $$P(D)=\dfrac{6/175}{3/25}=\dfrac{2}{7} \approx 29\,\%$$
$\square$

Hallar la probabilidad de que el número de caras obtenido sea ...

ENUNCIADO. Se lanza $5000$ veces una moneda. Se sabe que la probabilidad de que salga cara en un lanzamiento es del $60\,\%$. Calcular la probabilidad de obtener menos de $2500$ caras.

ENUNCIADO. Denotemos por $X$ la variable aleatoria número de caras obtenidas. La distribución de probabilidad natural de dicha variable es binomial: $B(5000\,,\,0'6)$; la esperanza matemática ( media ) de $X$ es $E[X]=n\cdot p=5000\cdot 0'6 = 3000$, por lo cual ya podemos avanzar que, como $2500$ es notablemente menor que dicha valor, la probabilidad pedida ha de ser muy pequeña, casi cero. Vamos a calcularla:

$$P\{X<2500\}=\displaystyle \sum_{i=0}^{2500-1}\,\binom{5000}{i}\cdot 0'6^{i}\cdot (1-0'6)^{5000-i}$$ Es manifiesta la enorme dificultad de cálculo con la distribución natural de $X$, lo cual hace del mismo algo inviable; por ello, y de acuerdo con el teorema de De Moivre-Laplace, procedemos a aproximar la variable binomial $X$ ( que es discreta ) por una variable normal $X'$ ( que tiene una d. continua ) de media $\mu=n\,p$ y desviación estándar $\sigma=\sqrt{n\, p\, q}=\sqrt{1200}$ ( donde la probabilidad de éxito ( en un lanzamiento ) es $p=0'6$ y, por tanto, la de fracaso, es $q=1-p=0'4$ ), pues se satisfacen las condiciones suficientes para ello: $n\cdot p = 5000 \cdot 0'6 = 3000 > 5$ y $n\cdot (1-p)= 5000 \cdot 0'4 = 2000 > 5$.

Los parámetros de la distribución normal de $X':N(\mu\,,\,\sigma)$ son $\mu=n\,p = 5000\cdot 0'6=3000$ y $\sigma=\sqrt{5000 \cdot 0'6 \cdot 0'4}=\sqrt{1200} \approx 34'6410$

Así, efectuando, también, la corrección de Yates o corrección de continuidad, podemos escribir
$P\{X \prec 2500\} \approx P\{X'< 2500+0'5\}=P\{X'<2500'5\}\overset{\text{tipificando} X}{=}$
$=P\{Z \prec \dfrac{2500'5-3000}{64'6410} \}=P\{Z \prec -14'4193\}$
$= P\{Z \ge 14'4193\}=1-P\{Z\prec 14'4193\} \approx 0$, ya que, para un valor de abscisa tan grande ( alrededor de $14$ ), $P\{Z \prec 14'4193\}\approx 1$

En conclusión, la probabilidad pedida, $P\{X \prec 2500\}$, resulta ser (prácticamente) cero, como era de esperar. $\square$

Probabilidad condicionada

ENUNCIADO. Dada una cierta experiencia aleatoria, se sabe que la probabilidad de que ocurra un cierto suceso, $A$, es igual a $\frac{1}{3}$; y, que la probabilidad de que ocurra otro suceso, $B$, sabiendo que ocurre el suceso $A$, es igual a $\frac{3}{4}$. ¿ Cuál es la probabilidad de que ocurran los dos sucesos ?.

SOLUCIÓN. De la definición de probabilidad condicionada,
$P(A|B)=\dfrac{P(A\cap B)}{P(B)}$, luego $P(A \cap B)=P(A|B)\cdot P(B)=\dfrac{3}{4}\cdot \dfrac{1}{3}=\dfrac{1}{4}$
$\square$

Se sabe que la distribución de la masa de las manzanas de un cierto cargamento es ...

ENUNCIADO. Se sabe que la distribución de la masa de las manzanas de un cierto cargamento es la de una variable aleatoria normal, cuya media es de $250\;\text{gramos}$ y cuya desviación estándar es de $30\;\text{gramos}$. Se elige, al azar, una manzana de dicho cargamento, ¿ cuál es la probabilidad de que la masa de dicha manzana esté comprendida entre $220$ y $260\;\text{gramos}$ ?.

SOLUCIÓN.
$X$ es $N(250\,,\,30)$, luego $P\{220 \le X \le 260\}$. Para poder utilizar las tablas de la distribución de probabilidad normal $N(0,1)$, realizamos la siguiente transformación de la variable

$$Z=\dfrac{X-250}{30}$$ De esta forma
$P\{220 \le X \le 260\} = P\{\dfrac{220-250}{30} \le Z \le \dfrac{260-250}{30}\}$
$=P\{-1 \le Z \le 0'3333\}$ ( habiendo aproximado la abscisa del extremo superior a la cuarta cifra decimal )

$=P\{Z \le 0'3333\}-P\{Z \le -1\}\overset{\text{simetría de} f(z)}{=}P\{Z \le 0'3333\}-P\{Z \ge 1\}$

$\overset{\text{prop. del contrario}}{=}P\{Z \le 0'3333\}-(1-P\{Z \le 1\})$

$=P\{Z \le 0'3333\}+P\{Z \le 1\}=F(0'3333)+F(1)-1 \quad \quad (1)$
siendo $F(z)$ la función de distribución de probabilidad, que viene en las tablas de $Z$ que es $N(0,1)$

Consultando las tablas, vemos a la abscisa $0'33$ le corresponde $F(0'33)=0'6293$; y, a la abscisa $0'34$, $F(0'34)=0'6331$. Entonces, como $0'33 \le 0'3333 \le 0'34$, realizando la interpolación lineal, $$\dfrac{F(0'3333)-0'6293}{0'3333-0'33}=\dfrac{0'6331-0'6293}{0'34-0'33}$$ de donde $$F(0'3333)=\dfrac{0'6331-0'6293}{0'34-0'33}\cdot (0'3333-0'33)+0'6293 \approx 0'6306$$

Por tanto, de (1), y consultando las tablas, obtenemos que la probabilidad pedida es $$0'6306+0'8413-1 = 0'4719 \approx 47\,\%$$
$\square$

De tarjetas y cajones

ENUNCIADO. Guardamos siete tarjetas, numeradas del uno al siete, en siete cajones ( numerados, también, del uno al siete ), poniendo cada tarjeta en el cajón de su respectivo número. Una vez han sido guardadas la tarjetas, alguien ha sacado la tarjeta número uno ( del cajón número 1 ) y, luego, la ha vuelto a guardar en uno de los siete cajones ( que elije al azar ). A continuación, sacamos una tarjeta del segundo cajón ( en dicho cajón, puede haber una sola tarjeta -- la número dos -- o bien dos, la número uno y la número dos ), ¿ cuál es la probabilidad de que la tarjeta que sacamos sea la número uno ?.

Sugerencia: Tener en cuenta el teorema de la Probabilidad Total.

SOLUCIÓN. Sean los siguientes sucesos:
    $C_2$: en la reubicación de la tarjeta número uno, poner la tarjeta número uno ( extraída del primer cajón ) en el cajón número dos
    $T_1$: en la extracción final de tarjeta del cajón número dos, extraer la tarjeta número uno del cajón número dos

Teniendo en cuenta que $\{C_2\,,\,\overline{C_2}\}$ constituye una partición del espacio muestral $\Omega$, podemos escribir que $$T_1=(T_1 \cap C_2) \cup (T_1 \cap \overline{C_2})$$ Y como $(T_1 \cap C_2)$ y $(T_1 \cap \overline{C_2})$ son sucesos incompatibles, $$P(T_1)= P\left(C_2 \cap T_1)\right) + P\left(\overline{C_2} \cap T_1 \right)$$ donde, teniendo en cuenta la definición de probabilidad condicionada, $$P(T_1 \cap C_2) = P(T_1|C_2)\cdot P(C_2)=\dfrac{1}{2}\cdot \dfrac{1}{7}=\dfrac{1}{14}$$
y
$$P(T_1 \cap \overline{C_2}) = P(T_1|\overline{C_2})\cdot P(\overline{C_2})=0\cdot \dfrac{6}{7}=0$$
Por consiguiente, la probabilidad pedida es igual a $$\dfrac{1}{14}+0=\dfrac{1}{14} \approx 7\,\%$$
$\square$

Sobre un juego de apuestas parecido al de la Bono Loto

Recomiendo que deis un vistazo a este problema de cálculo de probabilidades ( de 1.º de Bachillerado ).

Apuestas en el lanzamiento de dados. Un problema histórico.

¿ Qué es más probable: sacar al menos un seis al lanzar un dado cuatro veces, o bien sacar al menos dos seises al lanzar cuatro dados veinticuatro veces ?. Este problema es histórico, pues en la época en que se planteó y resolvió, empezaba a florecer el cálculo de probabilidades. Lo propuso el pensador, escritor y aficionado a los juegos de apuestas Antoine Gombaud ( chevalier de Mére ) [1607-1684], al matemático Blaise Pascal (1623-1662 ), quien lo resolvió. El resultado es que la probabilidad del primer supuesto es del $52\,\%$ [ver el cálculo], mientras que la del segundo es del $49\,\%$ [ ver el cálculo ]. Así que es mejor apostar a la primera opción.

Probabilidad de que aparezca al menos un doble seis al lanzar dos dados 24 veces

ENUNCIADO. Calcular la probabilidad de sacar al menos dos seises al lanzar dos dados veinticuatro veces.

SOLUCIÓN.
Al lanzar dos dados hay $6^2=36$ resultados posibles, de los cuales uno sólo corresponde a obtener dos seises, por lo que la probabilidad de sacar dos seises lanzando dos dados una vez es $\dfrac{1}{36}$; por consiguiente, la probabilidad de que no salgan dos seises es $1-\dfrac{1}{36}=\dfrac{35}{36}$. Ahora, al lanzar $24$ veces la pareja de dados, la probabilidad de que no aparezca ninguna vez el doble seis es $\left(\dfrac{35}{36}\right)^{24}$, luego la probabilidad del suceso contrario ( que al menos aparezca el doble seis una vez, esto es, que al menos aparezcan dos seises ) es $$1-\left(\dfrac{35}{36}\right)^{24} \approx 0,49 = 49\,\%$$.

$\square$

Sacar al menos un '6' al lanzar cuatro dados

ENUNCIADO. Calcular la probabilidad de sacar al menos un '6' al lanzar un dado cuatro veces.

SOLUCIÓN.
La probabilidad de sacar un '6' en un lanzamiento es $\dfrac{1}{6}$, luego la probabilidad de no sacarlo es $1-\dfrac{1}{6}=\dfrac{5}{6}$; por tanto, la probabilidad de que al lanzar un dado cuatro veces no aparezca el '6' en ninguna de ellos es $\left(\dfrac{5}{6}\right)^4$, y la probabilidad del suceso contrario a éste ( de que aparezca al menos un '6' ) es $1-\left(\dfrac{5}{6}\right)^4=\dfrac{671}{1296} \approx 0,52 = 52\,\%$. $\square$

Calcular las siguientes integrales definidas

ENUNCIADO. Calcular:

a) $\displaystyle \int_{-\infty}^{+\infty}\,e^{-\frac{x^2}{2}}\,dx$

b) $\displaystyle \int_{-1}^{1}\,e^{-\frac{x^2}{2}}\,dx$

SOLUCIÓN.
a) El integrando es la función de densidad de la distribución normal $N(0,1)$, y sabemos que $\dfrac{1}{\sqrt{2\pi}}\,\displaystyle \int_{-\infty}^{+\infty}\,e^{-\frac{x^2}{2}}\,dx=1$; por tanto, $$\displaystyle \int_{-\infty}^{+\infty}\,e^{-\frac{x^2}{2}}\,dx=\sqrt{2\pi}$$

b) Teniendo en cuenta lo dicho arriba, $\displaystyle \int_{-1}^{1}\,e^{-\frac{x^2}{2}}\,dx=F(1)-F(-1)$, siendo la función primitiva $F(x)$ la función de distribución de probabilidad de una variable aleatoria $N(0,1)$. Consultando las tablas de dicha función, encontramos $F(1) = 0,8413$ ( aproximada con $4$ cifras decimales ); teniendo en cuenta, además, la propiedad de simetría con respecto al eje de ordenadas de densidad $f(x)$ y la propiedad de la probabilidad del contrario, podemos escribir, $F(-1)=1-F(1)=1-0,8413$, luego se tiene que el valor de la integral pedida es $$F(1)-(1-F(1))=2\,F(1)-1=0,6826$$
$\square$

Un ejercicio sobre los modelos binomial e hipergeométrico de variable aleatoria discreta

ENUNCIADO. En una urna hay $10$ bolas ( de igual tamaño, masa y con la misma sensación al tacto ), de las cuales $6$ están pintadas de blanco y el resto de otros colores. Extraemos $4$ bolas al azar. Calcular la probabilidad de que entre éstas hay exactamente $2$ bolas blancas:
a) Sacando las cuatro bolas una a una, reemplazando la bola extraída en la urna antes de sacar la siguiente bola.
b) Sacando las cuatro bolas a la vez

ENUNCIADO.
a)
En el primer caso, las elecciones de bola son independientes, luego ya hemos visto en otros ejercicios parecidos que la probabilidad pedida ( aplicando la regla de Laplace, pues cada una de las $10$ puede escogerse con la misma probabilidad ) es igual al cociente entre el número de casos favorables al suceso por el que estamos interesados en el cálculo de su probabilidad y el número total de posibilidades, la probabilidad pedida es igual a $$\dfrac{\text{PR}_{4}^{2,2}\cdot \text{VR}_{6,2} \cdot \text{VR}_{10-6,2}}{\text{VR}_{10,4}} \approx 0,3456$$

Sin embargo, hay otra forma de calcular la probabilidad pedida, que consiste en utilizar el modelo binomial de variable aleatoria ( que funciona para pruebas repetidas independientes, con dos posibles resultados: "obtener bola blanca" o bien "obtener bola de color distinto al blanco". Denotemos por $X$ la v.a. números de bolas blancas que aparecen en el grupo de $4$ bolas extraídas, entonces $X=\{0,1,2,3,4\}$. Como en una extracción la probabilidad de sacar bola blanca es $\dfrac{6}{10}=0,6$ ( probabilidad de éxito ) y, por tanto, la probabilidad de nos sacar bola blanca es $1-0,6=0,4$, tenemos que $$P\{X=2\}=\binom{4}{2}\cdot (0,6)^2 \cdot (0,4^{4-2} \approx 0,3456$$

Nota 1: En las condiciones con las que hacemos las extracciones de bolas ( extracciones sucesivas independientes ), y para un caso general ( contemplando la posibilidad de cambiar los datos ) en que: $N$ represente el número de bolas de la urna; $N_b$ ( donde $N_b \le N $ ), el número de bolas de la urna que están pintadas de blanco; $m$ ( siendo $m \le N$ ), el número de bolas que extraemos; y, $m_b$, el de bolas que hay entre el grupo de $m$ bolas ( siendo $m_b \le m$ ) y que resultan ser blancas, podemos escribir que la probabilidad de que entre las $m$ bolas extraídas haya $m_b$ bolas blancas es igual a la función de probabilidad ( o de cuantía ) para $X=m_b$, esto es, $f_{\text{binomial}}(m_b)$; es decir,
$$P\{X=m_b\}=f_{\text{binomial}}(m_b)=\binom{m}{m_b }\cdot \left(\dfrac{N_b}{N}\right)^{m_b} \cdot \left(1-\dfrac{N_b}{N}\right)^{m-m_b}$$

b)
En este caso, podemos contemplar la extracción conjunta del grupo de $4$ bolas, como si se extrajesen ( también ) de forma sucesiva, pero sin reemplazar las bola que se ha sacado al ir a extraer la siguiente bola; decimos, por tanto, que estas extracciones sucesivas son dependientes. Al sacar las bolas de esta manera, la probabilidad pedida ( empleando nuevamente la regla de Laplace ) es igual a $$\displaystyle \dfrac{\binom{6}{2}\cdot \binom{10-6}{4-2}}{\binom{10}{4}} \approx 0,4826$$ Ello se ajusta a otro modelo de variables aleatoria: la distribución hipergeométrica.

Nota 2: En las condiciones con las que hacemos, ahora, las extracciones de bolas ( extracciones de unas cuantas bolas de forma simultánea ), y para un caso general ( por si cambiamos los datos ) en que ( como antes ): $N$ represente el número de bolas de la urna; $N_b$ ( donde $N_b \le N $ ), el número de bolas de la urna que están pintadas de blanco; $m$ ( siendo $m \le N$ ), el número de bolas que extraemos; y, $m_b$, el de bolas que hay entre el grupo de $m$ bolas ( siendo $m_b \le m$ ) y que resultan ser blancas, podemos escribir que la probabilidad de que entre las $m$ bolas extraídas haya $m_b$ bolas blancas es igual a la función de probabilidad ( o de cuantía ) para $X=m_b$, esto es, $f(m_b)$; es decir,
$$P\{X=m_b\}=f_{\text{hipergeométrica}}(m_b)=\dfrac{\binom{N_b}{m_b}\cdot \binom{N-N_b}{m-m_b}}{\binom{N}{m}}$$

$\square$

Ejercicios resueltos y comentados del examen de recuperación del 2.º trimestre ( temas: 5-9), realizado el día 31/03/2016

[ 1 | 2 | 3 | 4 ]

Ejercicio de integración

ENUNCIADO. Sea la función $f(x)=(x-1)^3$. Se pide:
a) Calcular la integral indefinida $\displaystyle \int\,f(x)\,dx$
b) Calcular la integral definida $\displaystyle \int_{0}^{2}\,f(x)\,dx$
c) Calcular el área delimitada por los siguientes elementos: la gráfica de la función, el eje de abscisas, y las rectas paralelas al eje de ordenadas que pasan por los puntos $A(0\,,\,-1)$ y $B(2\,,\,1)$

SOLUCIÓN.
a) $\displaystyle \int\,f(x)\,dx=\int\,(x-1)^3\,d(x-1)=\dfrac{1}{4}\,(x-1)^4+C$

b) Una primitiva de $f(x)$ es $F(x)=\dfrac{1}{4}\,(x-1)^4$, con lo cual, por el 2.º teorema fundamental del cálculo ( regla de Barrow ) podemos escribir
$$\displaystyle \int_{0}^{2}\,f(x)\,dx = F(2)-F(0)=\dfrac{1}{4}\,\left((2-1)^4\right)-\dfrac{1}{4}\,\left((0-1)^4\right)=\dfrac{1}{4}-\dfrac{1}{4}=0$$

c) La función $f(x)$ corta al eje de abscisas en $x=1$, luego el área pedida es igual a $$\displaystyle \left|\int_{0}^{1}\,f(x)\,dx\right|+\left|\int_{1}^{2}\,f(x)\,dx\right|$$
Y, como el dominio de integración es simétrico con respecto de la recta paralela al eje de ordenadas $x=1$, lo anterior es lo mismo que
$$\displaystyle 2 \cdot \left|\int_{0}^{1}\,f(x)\,dx\right|=2\cdot \left| F(1)-F(0)\right|=\dfrac{1}{2}$$
$\square$

Ecuación de la recta tangente a la gráfica de una función en un determinado punto

ENUNCIADO. Determinar la ecuación de la recta tangente a la gráfica de la función $f(x)=x^2+1$ en el punto $P$ de abscisa $x_P=-1$

SOLUCIÓN. La recta tangente a la gráfica de la función $f$ tiene por ecuación $$\text{r.t.}:y=m\,x+k$$ Por el significado geométrico de la derivada de una función en el punto $P$ $$m=f'(x_P)$$ derivando $$f'(x)=2x$$ luego $$m=f'(x_P=-1)=2\cdot (-1)=-2$$ Así, podemos escribir $$\text{r.t.}:y=-2\,x+k$$ Nos falta, ahora, determinar el valor de $k$; como $f(x_P)=(-2\,x_P+k)$ tenemos que $$(-1)^2+1=-2\cdot (-1)+k$$ esto es $$2=2+k$$ luego $$k=0$$ Por consiguiente $$\text{r.t.}:y=-2\,x+0$$ es decir $$\text{r.t.}:y=-2\,x$$

$\square$

Analizar y representar gráficamente

ENUNCIADO. Analizar y representar gráficamente la función $$f(x)=x^3+x^2-2x-2$$

SOLUCIÓN.
Nota: Me limito a poner los resultados, pues los pasos son análogos a los de este otro ejercicio.

$\square$

Máximos y mínimos

ENUNCIADO.
Considerar el conjunto de los rectángulos de perímetro igual a $2$ decímetros. Encontrar las dimensiones del rectángulo de dicho conjunto ( de rectángulos ) cuya área es máxima. ¿ Cuál es el valor de dicho máximo ?.

SOLUCIÓN.
Sean $x$ e $y$ el largo y el ancho de uno de dichos rectángulos. Sabemos ( por la información que se da en el enunciado sobre el valor del perímetro ) que $$2\,(x+y)=2$$ es decir $$x+y=1$$ y por tanto podemos expresar una lado en función del otro $$y=1-x$$ con lo cual, el área de un rectángulo cualquiera ( que cumpla la condición del enunciado ) viene dada por $$f(x)=x\,(1-x)$$

Forma de resolución 1.
Observemos que se trata de la función cuadrática, esto es, una función del tipo $f(x)=a\,x^2+b\,x+c$ ( que en el caso que nos ocupa es $$f(x)=-x^2+x$$ ) y su gráfica es una parábola cuyo vértice corresponde a un máximo ( ya que el coeficiente del término de grado dos, $a=-1$, es menor que cero ); basta, pues, con encontrar sus coordenadas empleando la fórmula ( conocida de cursos anteriores ) $x_V=-\dfrac{b}{2\,a}$ ( en nuestro caso: $a=-1$ y $b=1$ ), luego $$x_V=-\dfrac{-1}{2\cdot 1}=\dfrac{1}{2} \; \text{dm}$$ con lo cual $y_V=f(x_V)=f(\frac{1}{2})=-\left(\dfrac{1}{2}\right)^2+\dfrac{1}{2}=\dfrac{1}{2} \; \text{dm}$

Forma de resolución 2.
Hay, sin embargo, otro forma ( de más generalidad ) de encontrar el valor de $x$ que da el máximo -- más acorde con lo que estamos estudiando en este tema ( aplicaciones de la derivada ) -- y que consiste en imponer la condición de existencia de extremos relativos ( máximos y mínimos relativos ): $$f'(x)=0$$ entonces $$-2\,x+1=0 \Leftrightarrow x^*=\dfrac{1}{2}$$ Comprobemos ahora que se trata de un máximo relativo. Por el criterio del signo de la segunda derivada ( $f''(x)=-2$ para todo valor de $x$ del dominio de definición de la función ( que es continua y derivable en todos los puntos ) en dicho punto, vemos que ésta negativa ( por supuesto, también en $x=-\dfrac{1}{2}$ ), luego el extremo relativo encontrado corresponde a un máximo local. Además, dicho máximo es claro que es, también, el máximo absoluto de la función, que es el que estamos buscando.

En conclusión, como ya hemos justificado que dicho vértice corresponde a un máximo ( que es el máximo absoluto de la función ), el rectángulo de área máxima ( del conjunto de rectángulos propuesto ) es un cuadrado de $\dfrac{1}{2}$ decímetros de lado, y de área ( máxima ) igual a $\dfrac{1}{2}\cdot \dfrac{1}{2}=\dfrac{1}{4}\;\text{dm}^2$.
$\square$