Sea la región del plano dada por el sistema de desigualdades (...)

ENUNCIADO. Sea $S$ la región del plano definida por $$\left\{\begin{matrix}2x&-&y&\ge&1 \\ 2x&-&3y&\le&6 \\ x&+&2y&\ge&3 \\ x&+&y&\le&8 \\ &&y&\le&3\end{matrix}\right.$$
a) Represéntese la region $S$ y calcúlense las coordenadas de sus vértices
b) Obténganse los valores máximo y mínimo de la función $f(x,y)=2x+y$ en la región $S$, indicando los puntos en los cuales se alcanzan dichos valores máximo y mínimo.

SOLUCIÓN.

a)
Podemos expresar la desigualdades de la siguiente forma $$\left\{\begin{matrix} y \le 2x-1 \\ y \ge \dfrac{2}{3}x-2 \\ y \ge -\dfrac{1}{2}x+\dfrac{3}{2}\\ y \le -x+8 \\ y \le 3\end{matrix}\right.$$ que es más conveniente para encontrar la región $S$ ( convexa ) del plano.

Las ecuaciones de las rectas que contienen los lados de dicha región son $$\left\{\begin{matrix} y = 2x-1 \\ y = \dfrac{2}{3}x-2 \\ y = -\dfrac{1}{2}x+\dfrac{3}{2}\\ y = -x+8 \\ y = 3\end{matrix}\right.$$

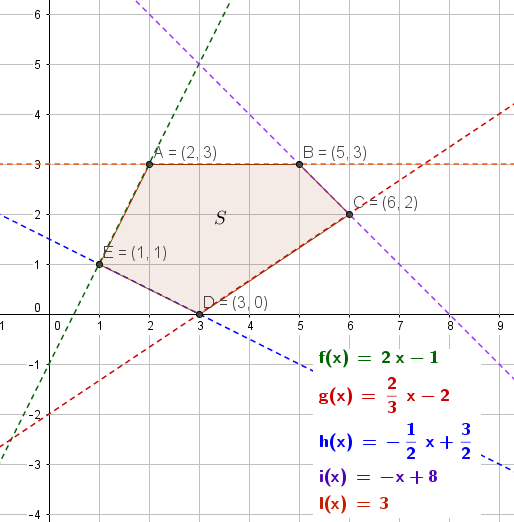
Representando dichas rectas en el plano y calculando los puntos de intersección de las mismas ( vértices de la región convexa $S$ ) obtenemos

b)
Despejando la variable dependiente $y$ de $f(x,y)\equiv k=2x+y$ se obtiene $y=-2x+k$, que representa una recta del haz de rectas paralelas de la función objetivo. El valor máximo ( respectivamente, mínimo ) de la ordenada en el origen $k$ es pues el valor máximo ( respectivamente, mínimo ) de $f$. Tal como se muestra en las siguientes figuras, hemos encontrado que el máximo corresponde a la recta del haz que pasa por $C(6,2)$, que es igual a $f(6,2)=14$; y, el mínimo, a la recta del haz que pasa por $E(1,1)$, y su valor es $f(1,1)=3$

$\square$