Calcular el área delimitada entre ...

ENUNCIADO
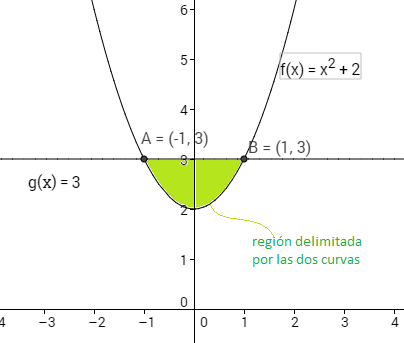
Calcular el área de la región delimitada por las gráficas de las funciones $f(x)=x^2+2$ y $g(x)=3$

SOLUCIÓN
Las abscisas de los puntos de intersección de las dos curvas vienen dadas por $$f(x)=g(x)$$ es decir $$x^2+2=3 \Leftrightarrow x=\pm 1$$ Por tanto el área pedida es igual a $$\left| \int_{-1}^{1} (f(x)-g(x))\,dx \right|$$ y como el dominio de integración es simétrico respecto del eje de ordenadas, esto es igual a $$2 \left| \,\int_{0}^{1} (f(x)-g(x))\,dx \right| = 2 \left|\,\int_{0}^{1} (3-(x^2+2))\,dx \right|=$$
$$=2 \left|\,\int_{0}^{1} (-x^2+1))\,dx\right|=2\,\left| \left[ -\dfrac{1}{3}\,x^3+x \right]_{0}^{1} \right|$$
$$=2\left((-\dfrac{1}{3}\cdot 1^3+1)-(0+0)\right)=2\,(-\dfrac{1}{3}+1)=2\cdot \dfrac{2}{3}=\dfrac{4}{3}$$

$\square$

[nota del autor]