Un blog con cuestiones, ejercicios, problemas, aplicaciones y comentarios relacionados con los contenidos de Matemáticas del segundo curso de Bachillerato en la modalidad de Ciencias Sociales
viernes, 29 de mayo de 2015
(...) ¿ Cuántas unidades deben ponerse a la venta para que haya equilibrio entre la oferta y la demanda ?
Considérese la función de demanda $g(x)=\dfrac{100}{x+1}$, donde $x$ denota el número artículos demandados ( en millares de unidades ), y $g(x)$ viene expresada en euros por cada millar de unidades. Mediante un estudio de mercado, se ha llegado a la conclusión de que el precio ( en euros ) por millar de unidades se ajusta a la función $f(x)=x+1$ ( modelo de oferta ). ¿ Cuál es el dominio que debemos considerar para la función de oferta ? ¿ Cuántas unidades deben ponerse a la venta para que haya equilibrio entre la oferta y la demanda ? ¿ Cuál es el precio unitario de este artículo en el punto de equilibrio ?.
SOLUCIÓN
Atendiendo al significado del modelo matemático, el dominio de la función $g(x)$ es $[0,\,\,+\infty)$ ( en millares de unidades ). Los puntos de equilibrio vienen dado por la intersección de ambas curvas, luego deben satisfacer la siguiente ecuación, $g(x)=f(x)$, es decir $$\dfrac{100}{x+1}=x+1 \Leftrightarrow (x+1)^2=100$$ de lo cual deducimos que $x=9$ millares de unidades y $f(x)=9+1=10$ euros por cada mil unidades.
$\square$
miércoles, 27 de mayo de 2015
Calcular el área delimitada por las siguientes curvas ...
Calcular el área de la región del plano delimitada por las curvas $f(x))=x^2-3$ y $g(x)=-(x-1)^2+1$
SOLUCIÓN:
El área pedida es igual a $$\left| \int_{x_A}^{x_B}\,(f(x)-g(x)\,dx \right|$$ es decir $$\left| \int_{x_A}^{x_B}\,(2x^2-2x-3)\,dx \right|$$ siendo los límites de integración, $x_A$ y $x_B$, las soluciones de la ecuación $$f(x)=g(x)$$ esto es $$x^2-3=-(x-1)^2+1$$ que resultan ser $$x_A=\dfrac{2-\sqrt{28}}{4} \; \text{y}\;x_A=\dfrac{2+\sqrt{28}}{4}$$ Aplicando la regla de Barrow obtenemos $$\left| \left[ \dfrac{2}{3}\,x^3-x^2-3x \right]_{x_A}^{x_B}\right|$$ esto es $$\left| \dfrac{2}{3}\,(x_{B}^3-x_{A}^3)-(x_{B}^2-x_{A}^2)-3\,(x_{B}-x_{A}) \right| \approx \left|-6,17\right|=6,17$$
$\square$
Calcular el área delimitada entre ...
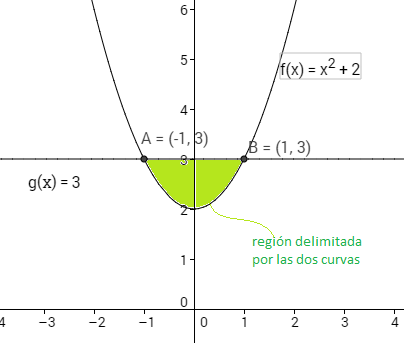
Calcular el área de la región delimitada por las gráficas de las funciones $f(x)=x^2+2$ y $g(x)=3$
SOLUCIÓN
Las abscisas de los puntos de intersección de las dos curvas vienen dadas por $$f(x)=g(x)$$ es decir $$x^2+2=3 \Leftrightarrow x=\pm 1$$ Por tanto el área pedida es igual a $$\left| \int_{-1}^{1} (f(x)-g(x))\,dx \right|$$ y como el dominio de integración es simétrico respecto del eje de ordenadas, esto es igual a $$2 \left| \,\int_{0}^{1} (f(x)-g(x))\,dx \right| = 2 \left|\,\int_{0}^{1} (3-(x^2+2))\,dx \right|=$$
$$=2 \left|\,\int_{0}^{1} (-x^2+1))\,dx\right|=2\,\left| \left[ -\dfrac{1}{3}\,x^3+x \right]_{0}^{1} \right|$$
$$=2\left((-\dfrac{1}{3}\cdot 1^3+1)-(0+0)\right)=2\,(-\dfrac{1}{3}+1)=2\cdot \dfrac{2}{3}=\dfrac{4}{3}$$
$\square$
martes, 26 de mayo de 2015
Calcular el siguiente límite
Calcular el límite $$\displaystyle \lim_{x \rightarrow 0}\,\left(x\,\sin{(\dfrac{1}{x})}\right)$$
SOLUCIÓN
Démonos cuenta de que, al pasar al límite, el factor $x$ del argumento del límite tiende a $0$, permaneciendo el segundo factor, $\sin{(\dfrac{1}{x}}$, acotado entre $-1$ y $1$; por lo tanto $$\displaystyle \lim_{x \rightarrow 0}\,\left(x\,\sin{(\dfrac{1}{x})}\right)=0$$
$\square$
lunes, 25 de mayo de 2015
El precio de coste de un cierto artículo ...
El precio de coste de un cierto artículo es de $80$ euros. Se sabe que si el precio de venta del mismo es de $130$ euros, el número de ventas es igual a $1000$; y, además, se observa que por cada euro que aumente o disminuya el precio de venta, el número de ventas disminuye o aumenta, respectivamente, en $60$. ¿ Cuál es el precio de venta que maximiza los beneficios ? ¿Cuántas unidades de dicho artículo se venderán con dicho precio de venta? ¿Cuál es el beneficio ( máximo ) que se obtendrá en estas condiciones ?.
SOLUCIÓN
Denotemos por $n$ el número de ventas y por $x$ el precio de venta. Estas variables estan ligadas por la función lineal afín $n(x)=-60x+k$. Calculemos el valor de la ordenada en el origen, $k$; para ello, impongamos que para $x=130$, $n=1000$; por tanto, $1000=-60\cdot 130+k$, de donde obtenemos $k=8800$; así, pues, $n=-60x+8800$. Con esto, podemos expresar la función de beneficios, $f$, en función de $x$; en efecto, como, por definición, el beneficio es igual a los ingresos debidos a las ventas menos los gastos debidos a los costes, $f(x)=(-60x+8800)(x-80)$. Imponiendo la condición necesaria de existencia de extremos relativos, $f'(x)=0$, obtenemos $$-60(x-80)+(8800-60x)=0$$ de donde, despejando $x$, se llega a $$-120x+13600=0 \Leftrightarrow x = \dfrac{1360}{12} \approx 113,33 \; \text{euros}$$ Se comprueba que se trata de un máximo por ser la función $f(x)$ una función polinómica de segundo grado ( dicho extremo corresponde a la abscisa del vértice ), y al ser negativo el coeficiente del término de grado dos, no puede corresponder éste sino a un máximo. Además, es el máximo absoluto de la función, dada la naturaleza de ésta.
El número de unidades que se venderán, en estas condiciones, es igual a $n(\dfrac{1360}{12})=-60\cdot \dfrac{1360}{12}+8800=2000\;\text{unidades}$.
El máximo beneficio, en estas condiciones, es igual a $f\left(\dfrac{1360}{12}\right)=(-60\cdot \dfrac{1360}{12}+8800)(\dfrac{1360}{12}-80)\approx 66\,666,67\; \text{euros}$
$\square$
Un barco se desplaza a ...
Un barco que se desplaza a velocidad constante, $v$ ( en kilómetros por hora ), consume $200 +0,1\,v^3$ litros de combustible cada hora. ¿ A qué velocidad debe desplazarse a fin de minimizar el gasto de combustible al realizar un trayecto de $d$ kilómetros ?.
SOLUCIÓN
El tiempo que dura la navegación ( en horas ) es $d/v$, luego el gasto de combustible ( para realizar el trayecto ) en función de la velocidad es $$f(v)=\dfrac{d}{v}\,(200+0,1\,v^3)$$ esto es $$f(v)=d\,(\dfrac{200}{v}+0,1\,v^2)$$
Imponiendo la condición necesaria de extremos relativos $$f'(v)=0$$ obtenemos $$-\dfrac{200}{v^2}+0,2v=0 \Leftrightarrow -200+0,1\,v^3=0 \Leftrightarrow v=\sqrt[3]{1000}=10\,\dfrac{\text{km}}{\text{h}}$$
Comprobemos que se trata de un mínimo local; para ello, utilizaremos aquí el criterio de la segunda derivada. Derivando la función derivada obtenemos la función segunda derivada $$f''(v)=\dfrac{400}{v^3+0,2}$$ cuyo valor para el punto crítico es positivo $$f''(10)=\dfrac{400}{1000}+0,2 \succ 0$$
con lo cual queda demostrado que la velocidad encontrada corresponde a un mínimo relativo de $f(v)$; además, como la función está definida sólo para $v \succ 0$, y $\displaystyle \lim_{v \rightarrow \infty}\,f(v)=+\infty$, dicho mínimo relativo es el mínimo absoluto de la función lo cual puede visualizarse también en la gráfica de la función:
El gasto mínimo de combustible es por tanto, $f(10)=30d$.
$\square$
Una persona invierte ...
Una persona invierte un total de $7000$ euros en acciones de las empresas A y B y en un depósito a $12$ meses al $1\,\%$. Pasado un año, vende sus acciones, obteniendo una [rentabilidad] del $5\,\%$ en las acciones de la empresa A y del $3\,\%$ en las de B. El beneficio total de sus tres inversiones es $202$ euros. Determinar qué cantidad destinó a cada inversión si sabemos que el dinero total destinado a comprar acciones superó en $2600$ al dinero del depósito.
SOLUCIÓN
Denotando por $x$ a la inversión en acciones de la empresa A; $y$, a la inversión en acciones de la empresa B; y, $z$ al depósito a $12$ meses, podemos plantear el siguiente sistema de ecuaciones $$\left\{\begin{matrix}
x & + & y & + & z & = 7000\\
0,05x & + & 0,03y & + & 0,01z & = 202\\
x & + & y & - & z & = 2600\\
\end{matrix}\right.$$ es decir $$\left\{\begin{matrix}
x & + & y & + & z & = 7000\\
5x & + & 3y & + & z & = 20200\\
x & + & y & - & z & = 2600\\
\end{matrix}\right.$$
Procedemos a reducirlo por Gauss. Restando la primera ecuación de la tercera y sustituyendo ésta por el resultado de dicha operación obtenemos ( simplificando esta última ) el sistema equivalente $$\left\{\begin{matrix}
x & + & y & + & z & = 7000\\
5x & + & 3y & + & z & = 20200\\
& & & & z & =2200\\
\end{matrix}\right.$$
Multiplicando por $-5$ la primera ecuación y sumando a la segunda, miembro a miembro, y simplficando, obtenemos el sistema equivalente $$\left\{\begin{matrix}
x & + & y & + & z & = 7000\\
& + & y & + & 2z & = 7400\\
& & & & z & =2200\\
\end{matrix}\right.$$
Vemos así que el rango del sistema de ecuaciones es $3$ y que es igual al número de incógnitas, luego el sistema es compatible determinado ( como cabría esperar ). Sustituyendo y despejando hacia arriba, a partir del resultado de la última ecuación, $z=2200\;\text{euros}$, obtenemos: $y=3000\;\text{euros}$, y $x=1800\,\text{euros}$. $\square$
En un cierto instante, un apersona empieza a propagar un rumor ...
Una persona empieza a propagar un rumor en un grupo de mil personas en el instante inicial ( $t=0$ horas ). Se sabe que dicho rumor se difunde a un ritmo que viene dado por la función $f(t)=2^t$ ( personas por hora ). Se pide:
a) ¿ Cuál es la función que expresa el número de personas que están al corriente del rumor en cada instante de tiempo ?
b) ¿ Cuál es el porcentaje de la población que conoce el rumor al cabo de $8$ horas ?
SOLUCIÓN
a) La función pedida, que denotamos por $F(t)$, es una primitiva de la función que expresa el ritmo de difusión del rumor, $f(t)$; y, para determinarla, hallaremos primero la familia de funciones primitivas de $f$, esto es, la integral indefinida de $f(t)$ $$\int\,f(t)\,dt = \int \,2^t\,dt = \dfrac{1}{\ln{2}}\,2^t+C \quad \quad (1)$$
Para calcular el valor de la constante de integración, imponemos la condición $F(0)=1$, con lo cual $$1=\dfrac{1}{\ln{2}}\cdot 2^0 + C$$ despejando $C$, obtenemos $$C=1-\dfrac{1}{ln{2}}$$ Sustituyendo el valor de la constante en (1) obtenemos la función pedida $$F(t)=\dfrac{1}{\ln{2}}(2^t-1)+1$$
b) El número de personas a las que les ha llegado el rumor ( incluyendo a la persona que lo propagó ) al cabo de $8$ horas es igual a $$F(8)=\dfrac{1}{\ln{2}}(2^8-1)+1=\dfrac{255}{\ln{2}}+1 \approx 369 \,\text{personas}$$
Observación:
Otra forma de calcular esto es la siguiente: el número de personas que han sido objeto de la transmisión del rumor al cabo de $8$ horas es $$\displaystyle \int_{0}^{8}\,2^t\,dt$$ que es igual a $$\left[\dfrac{1}{\ln{2}}\,2^t \right]_{0}^{8}=\dfrac{255}{\ln{2}}\approx 368$$
Ahora bien, sumando a esta cantidad la persona que lo ha transmitido, obtenemos el resultado calculado de la primera forma, $369$ personas. Por consiguiente, el porcentaje pedido es $\dfrac{369}{1000}=36'9 \,\%$ $\square$
viernes, 22 de mayo de 2015
Una muestra aleatoria simple ...
a) Un intervalo de confianza de $\mu$, al $90\,\%$ de confianza, sabiendo que la desviación estándar de la población, $\sigma$, es igual a $0'8$ años.
b) El valor del error que se comete al estimar, de ese modo, el parámetro $\mu$
SOLUCIÓN.
a)
Por el Teorema Central del Límite, la variable aleatoria "edad", $X \sim N(\mu\,,\,\sigma/\sqrt{n})$, siendo $n$ es el tamaño de la muestra ( $n=100$ ) y $\sigma/\sqrt{n}$ la desviación en el muestreo del estimador de la media muestral, $\bar{x}$ ( que denotamos por $\sigma(\bar{x})$. Así, al ser $\sigma=0'8$, $\sigma/\sqrt{n}=0'8/10=0'08$, la distribución de $X$ es $N(\mu\,,\,0'08)$.
El intervalo de confianza en la estimación de $\mu$ es, por tanto, $I=(\bar{x}-E\,,\,\bar{x}+E)$ (1), donde la mitad de la longitud del intervalo, centrado en $\bar{x}$, representa una cota del error pedido, que, como ya sabemos, es igual a $E=z_{\alpha/2}\,\sigma(\bar{x})$ (2), que se pide explícitamente en el segundo apartado.
Necesitamos, por tanto, determinar el valor de la abscisa $z_{\alpha/2}$; para ello, utilizamos las tablas de la variable normalizada/tipificada $Z$, que es $N(0,1)$. Procedemos a ello: como el nivel de confianza, $1-\alpha$, es igual a $0'9$ ( en tanto por unidad ), encontramos que $\alpha/2=(1-0'9)/2=0'05$ ( por ser simétrica la función de densidad $f(z)$ respecto del eje de ordenadas ); teniendo en cuenta que $P\{Z \le z_{0'05}=1-0'05=0'95$ y consultando este valor en el interior de las tablas, encontramos el valor de la abscisa crítica correspondiente, $z_{0'05} \approx 1'65$.
Por tanto, de (1), encontramos que el intervalo de confianza para $\mu$, al $90\,\%$ de confianza es $$I=(18'7-1'65\cdot0'08\,,\,18'7+1'65\cdot0'08)$$ esto es $$I=(18'5\,,\,18'9)$$
b)
El error, $E$, que corresponde a dicho intervalo de confianza ( que ya hemos empleado al calcular los extremos del mismo ) es igual, de (2), a $1'65 \cdot 0'08 = 0'132 \prec 0'2$ años.
Nota: En otras palabras, podemos afirmar que la media $\mu$ de la edad de la población de estudiantes ( que se presenta al examen ) es igual a $\bar{x} \pm E$ con un nivel de confianza $1-\alpha$; en concreto: la media $\mu$ de la edad de la población de estudiantes ( que se presenta al examen ) es igual a $18'7 \pm 0'2$ con un nivel de confianza del $90\,\%$
$\square$
Resolver el siguiente ejerccio de programación lineal
$$\left\{\begin{matrix}
x & \ge & 0\\
y & \ge & 3\\
x+y & \le & 10\\
2y & \ge & 3x\\
\end{matrix}\right.$$
¿ En qué puntos de la región alcanza el máximo y el mínimo la función objetivo $f(x,y)=4x+3y$ ? ¿ Cuáles son los valores de función en dichos puntos ?.
SOLUCIÓN.
El siguiente gráfico ( realizado con Geogebra ) ilustra el resumen de la resolución del problema
La ordenada en el origen, $k$, de cada una de las rectas de la familia de la función objetivo, representa el valor de $\dfrac{1}{3}\cdot F(x_P,y_P)$, para cada punto $P(x_P,y_P)$ de la región factible; evidentemente, el máximo de $k$ se da para el mismo punto que el máximo de $F(x,y)$, y lo propio podemos decir en cuanto al mínimo. Así, examinando el gráfico, puede verse que el máximo de $F(x,y)$ lo da el punto $C(4,6)$, que es igual a $F(4,6)=4\cdot 4 + 3 \cdot 6 = 34$, y el valor mínimo lo da el punto $A(0,3)$, que es igual a $F(0,3)=4\cdot 0+3 \cdot 3=9$.
Nota: la barra deslizadora de la imagen permite, con Geogebra, hacer que las rectas de la función objetivo recorran los puntos de la región factible.
$\square$
Sea el sistema de ecuaciones lineales ...
$$\left\{\begin{matrix}
x &+ &y &+& z& = & 1 \\
x &- &y &-& z& = & 0 \\
x &+ &y &+& m\,z& = & -1 \\
\end{matrix}\right.$$
Se pide:
a) Analizar el sistema en función de los valores que tome el parámetro $m \in \mathbb{R}$
b) Resolver el sistema para $m:=-1$
SOLUCIÓN.
a)
Reduciendo el sistema por Gauss ( $f_1-f_2 \rightarrow f_2$; $f_1-f_3 \rightarrow f_3$ ) obtenemos el siguiente sistema equivalente al original $$\left\{\begin{matrix}
x &+ &y &+& z& = & 1 \\
& &2y &+& 2z& = & 1 \\
& & &+& (1-m)\,z& = & -1 \\
\end{matrix}\right.$$
de donde deducimos que en el caso de que $1-m$ sea cero ( y por tanto, $m$ sea igual a $1$ ), el sistema es incompatible ya que se llega así a una contradicción ( $0 = -1$ ); por lo tanto, el sistema es incompatible para $m=1$. Para cualquier otro valor de $m$ las tres ecuaciones son linelamente independientes: el rango del sistema es $3$, valor que es igual al número de incógnitas; así, pues, por el Teorema de Rouché-Fröbenius, el sistema es compatible determinado para todo valor de $m$ distinto de $1$.
b)
Teniendo en cuenta, ahora, el valor de $m$ ha de ser ( condición del enunciado ) igual a $-1$, el sistema de ecuaciones a resolver ( ya reducido ) es $$\left\{\begin{matrix}
x &+ &y &+& z& = & 1 \\
& &2y &+& 2z& = & 1 \\
& & &+& 2z& = & -1 \\
\end{matrix}\right.$$
que, como ya se ha demostrado, tiene solución única ( por ser $m \neq 1 $ ). Entonces, despejando $z$ de la última ecuación, obtenemos $z=-\dfrac{1}{2}$; sustituyendo este valor en la segunda ecuación y despejando $y$, llegamos a $y=1$; y, finalmente, sustituyendo los valores de $x$ e $y$, que hemos encontrado en los dos pasos anteriores, en la primera ecuación, y despejando $x$, vemos que $x=\dfrac{1}{2}$.
$\square$
Expresar el número $a$ como suma de ...
SOLUCIÓN. Denotando por $x$ uno de los dos sumandos, podemos expresar la función producto de los dos como $$f(x)=x\,(a-x)$$
Imponiendo la condición necesaria de existencia de extremos relativos, $f'(x)=0$, encontramos $$a-2x=0 \Leftrightarrow x=\dfrac{a}{2}$$
abscisa que corresponde a un máximo relativo de la función, ya que, por el criterio del signo de la segunda derivada, $f''(x)=-2 \prec 0$. Además, dicho máximo relativo/local es el máximo absoluto de la función, por ser ésta una función polinómica de segundo grado y corresponder dicho extremo relativo a la abscisa del vértice. Así, pues, el valor máximo de la función pedida es $f \left( \dfrac{a}{2}\right)=\dfrac{a}{2}\,\left( a-\dfrac{a}{2}\right)=\left( \dfrac{a}{2} \right)^2$
$\square$
Sea la función ...
a) Analizar y dibujar la gráfica de la función
b) Calcular una primitiva de la función $g(x):=f(x)+\dfrac{1}{x^2}$
c) Calcular la integral definida $\displaystyle \int_{-1}^{1}\,g(x)\,dx$
SOLUCIÓN.
a)
i) Dominio de definición de la función:
Al anularse el denominador ( y no el numerador ) para $x=0$, la función no está definida en dicho punto, luego $D_f=\mathbb{R} \setminus\{0\}$
ii) Raíces ( ceros ) de la función:
El conjunto de valores de la variable independiente cuya imagen es cero se determina resolviendo dicha condición, $f(x)=0$, es decir $$\dfrac{x^3-1}{x^2}=0\Leftrightarrow x^3-1=0 \Leftrightarrow x=1$$
así, pues, existe una única raíz: $x=1$
iii) Ordenada en el origen de la función:
Por lo dicho en relación al dominio de definición, se desprende de ello que la gráfica de la función no corta al eje de ordenadas a distancia finita.
iv) Recorrido de la función:
Observemos que $\displaystyle \lim_{x \rightarrow +\infty}\,f(x)=+\infty$ y $\displaystyle \lim_{x \rightarrow -\infty}\,f(x)=-\infty$, de lo que se deduce que $\text{Recorrido}_f = \mathbb{R}$
v) Extremos relativos:
Imponiendo la condición necesaria de extremos relativos, $f'(x)=0$, obtendremos una ecuación cuyas soluciones son las abscisas de dichos puntos de la gráfica $$f'(x)=1+\dfrac{3}{x^3}=0 \Leftrightarrow x=(-3)^{\frac{1}{3}} \approx -1,4$$; y su ordenada es $f\left( (-3)^{\frac{1}{3}} \right) = - 4\cdot 3^{-\frac{2}{3}} \approx -1,9$. Veamos qué tipo de extremo relativo es; para ello utilizaremos el criterio del signo de la segunda derivada. Derivando la función primera derivada, obtenemos la función segunda derivada, $$f''(x)=-\dfrac{12}{x^4}$$ y su valor para $x= (-3)^{\frac{1}{3}} $ es $f''\left( (-3)^{\frac{1}{3}} \right) = - \dfrac{12}{(-3)^{\frac{4}{3}}} \prec 0$, luego se trata de un máximo local. Hay, por tanto, un máximo local/relativo en el punto de la gráfica $M=\left( (-3)^{\frac{1}{3}} \,,\,- 4\cdot 3^{-\frac{2}{3}}\right)$
vi) Intervalos de crecimiento y decrecimiento:
Teniendo en cuenta lo que hemos hecho en el apartado anterior, vemos que la derivada primera es positiva en todos los puntos del intervalo $(-\infty\,,\, (-3)^{\frac{1}{3}} ) \subset D_f$ y del intervalo $( 0\,,\,+\infty) \subset D_f$, luego la función crece en ambos intervalos; por otra parte, la derivada primera es negativa en los puntos del intervalo $((-3)^{\frac{1}{3}}\,,\,0 ) \subset D_f$, luego la función es decreciente en todos los puntos de dicho intervalo.
vii) Puntos de inflexión:
No hay, puesto que la función segunda derivada, $f''(x)=-\dfrac{12}{x^4}$, no se anula en ningún punto; así, pues, teniendo en cuenta el carácter del extremo relativo ( que es el mismo que el de los demás puntos, salvo $x=0$, en la que la función no está definida ), podemos afirmar que la función es cóncava en todo el dominio de definición.
viii) Rectas asíntotas verticales:
Teniendo en cuenta que $\displaystyle \lim_{x \rightarrow 0} = -\infty$, la función $f(x)$ presenta una asíntota vertical cuya ecuación es $x=0$, que es el eje de ordenadas.
ix) Rectas asíntotas oblicuas:
Las asíntotas oblicuas son del tipo $y=mx+k$, y, por tanto, incluyen - si las hubiese - las asíntotas horizontales. Empezamos calculando el valor de la pendiente: Por definición, $\displaystyle m=\lim_{x \rightarrow \infty}\,f'(x)$, o lo que es equivalente - forma que es más conveniente adoptar en este caso, por facilitar el cálculo, dada la naturaleza de la función - $$\displaystyle m=\lim_{x \rightarrow \infty}\,\dfrac{f(x)}{x} = \lim_{x \rightarrow \infty}\,\dfrac{x^3-1}{x^3}=\lim_{x \rightarrow \infty}\,(1-\dfrac{1}{x^3})=1-0=1$$
A continuación, calculamos la ordenada en el origen, $k$, que por definición es igual al valor del siguiente límite $$k=\displaystyle \lim_{x \rightarrow \infty}\,( f(x)-m\,x)=\lim_{x \rightarrow \infty}\,( \dfrac{x^3-1}{x^2}-1 \cdot x) = \lim_{x \rightarrow \infty}\,( \dfrac{x^3-1-x^3}{x^2})=\lim_{x \rightarrow \infty}\,( \dfrac{1}{x^2})=0$$ por consiguiente, hay una sóla asíntota vertical, de ecuación $y=x$
x) Gráfica de la función:
Reuniendo los elementos analizados podemos dibujar el siguiente trazo
b)
La familia de funciones primitivas ( integral indefinida ) de $g(x)$ viene dada por $\displaystyle \int \, \left( \dfrac{x^3-1}{x^2}+\dfrac{1}{x^2}\right)\,dx=\int\,\left( \dfrac{x^3}{x^2}-\dfrac{1}{x^2}+\dfrac{1}{x^2}\right)\,dx=\int\,\dfrac{x^3}{x^2}\,dx$
$=\int\,x\,dx=\dfrac{1}{2}\,x^2 + C$ ( Primer Teorema Fundamental del Cálculo ), donde $C$ es la constante de integración. Asignando un valor cualquiera a dicha constante, tenemos una función primitiva, tal como se pide en el enunciado; por ejemplo, si $C:=0$, podemos dar como resultado: $\dfrac{1}{2}\,x^2$
c)
Por el Segundo Teorema Fundamental del Cálculo, y siendo $G(x)=\dfrac{1}{2}\,x^2$ ( apartado anterior ), $$\displaystyle \int_{-1}^{1}\,g(x)\,dx=G(1)-G(-1)=\dfrac{1}{2}\cdot 1^2-\dfrac{1}{2}\cdot (-1)^2=0$$
Nota: al ser simétrico el dominio de integración y por ser la función integrando, $g(x)$, una función impar, podríamos habernos ahorrado el cálculo y afirmar, por ello, que la integral definida es cero. $\square$
lunes, 18 de mayo de 2015
Derivadas de las funciones $e^x$ y $\ln{x}$
Justificar que la derivada de la función $f(x)=e^x$ es la propia función exponencial; y que, teniendo en cuenta este resultado, la derivada de la función $\ln(x)$ es $\dfrac{1}{x}$
SOLUCIÓN:
(1)
Por la definición de derivada $$\displaystyle f'(x)=\lim_{\Delta x \rightarrow 0}\,\dfrac{f(x+\Delta x)-f(x)}{\Delta x}$$ tenemos que $$\displaystyle f'(x)=\lim_{\Delta x \rightarrow 0}\,\dfrac{e^{x+\Delta x}-e^{\Delta x}}{\Delta x}=\lim_{\Delta x \rightarrow 0}\,\dfrac{e^{x}\,e^{\Delta x}-e^{\Delta x}}{\Delta x}=e^{x}\,\lim_{\Delta x \rightarrow 0}\,\dfrac{e^{\Delta x}-1}{\Delta x}$$ al pasar ahora al límite, nos encontramos con una indeterminación del tipo $\dfrac{0}{0}$, que deshacemos teniendo en cuenta que $e^{\Delta x}-1$ y $\Delta x$ son infinitésimos equivalentes, con lo cual el valor del límite es $1$, y, por tanto, obtenemos $f'(x)=e^x$, como queríamos probar.
(2)
Teniendo en cuenta, ahora, este resultado, vamos a probar que $(\ln{x})'=\dfrac{1}{x}$. En efecto, las funciones $\ln{x}$ y $e^{x}$ son mutuamente recíprocas; esto es, si $y=e^x$, entonces $x=\ln{y}$. Y, por la propiedad de la derivada de la función recíproca, $x'_y=\dfrac{1}{y'_x}$, y, por tanto, $x'_y=\dfrac{1}{(e^x)'}=\dfrac{1}{e^x}=\dfrac{1}{e^{\ln{y}}}=\dfrac{1}{x}$
$\square$
miércoles, 13 de mayo de 2015
Dibujar la gráfica de la siguiente función y describir los elementos del análisis de la misma
Dibujar la gráfica de la función $f(x)=(x-1)^3+2$ empleando transformaciones geométricas de la gráfica de la parábola semicúbica $y=x^3$. A continuación, y a la vista del gráfico, hacer una descripción de los siguientes elementos de dicha función: dominio de existencia y recorrido, raíces, ordenada en el origen, puntos de inflexión, extremos relativos, intervalos de crecimiento/decrecimiento, intervalos de concavidad/convexidad, etcétera.
SOLUCIÓN:
a) Al tratarse de una función polinómica, $D_f=\mathbb{R}$ y $\text{Recorrido}_f=\mathbb{R}$; es continua en todos los puntos de su dominio de existencia - y por tanto no tiene asíntotas -, y es derivable en todos los puntos de su dominio de existencia ( Nota: Para darnos cuenta de lo que acabamos de decir, no es necesario visualizar la gráfica ).
Procedemos, ahora, a realizar la representación gráfica, tal como se nos ha indicado en el enunciado:
1º) Gráfica de $y=x^3$ ( parábola semicúbica centrada en el origen de coordenadas )
2º) Gráfica del trazo anterior, trasladado una unidad a la derecha, en la dirección del eje de abscisas
3º) Gráfica del trazo anterior, trasladado dos unidades en la dirección del eje de ordenadas ( en el sentido positivo )
Describiendo la gráfica resultante ( la última ), podemos afirmar que:
b) La función tiene una única raíz, en el intervalo $[-0'5,0]$
c) Tiene un punto de inflexión en el punto $(1,2)$
d) No tiene extremos relativos
e) La función es creciente en todo los puntos de su dominio de definición
f) Es cóncava en el intervalo $(-\infty\,,\,1)$
g) Es convexa en el intervalo $(1\,,\,+\infty)$
$\square$
Decir razonadamente si la función dada es continua y derivable en el siguiente punto ...
Decir, razonadamente, si la función $$f(x)=\left\{\begin{matrix}
x^2& \text{si}&x \le 1 \\
1& \text{si}&x = 1 \\
\end{matrix}\right.$$
es:
a) continua en el punto de abscisa $x=1$
b) derivable en el punto de abscisa $x=1$
SOLUCIÓN:
Representando la función definida a trozos, obtenemos la siguiente gráfica
con lo cual, la respuesta a la primera pregunta es afirmativa, por ser dicho trazo continuo. En cuanto a la segunda pregunta, la respuesta es NO. En efecto, la pendiente de la recta tangente al trazo a la izquierda de $x=1$ ( tramo de parábola ) en el punto $(1,f(1))$ es $f'(1)=2x |_{x=1}=2\cdot 1 = 2$; sin embargo, la pendiente de la recta tangente a la derecha de $x=1$ es $0$, por tratarse de un tramo con ordenada constante. Así, al no coincidir en dicho punto ambas pendientes de las respectivas rectas tangentes, podemos afirmar que no existe la derivada en dicho punto. $\square$
Demostrar que la siguiente función tiene por lo menos una raíz en ...
Utilizar el Teorema de Bolzano para demostrar que la función $f(x)=x^4-2$ tiene por lo menos una raíz en el intervalo $[0,2] \subset \mathbb{R}$
SOLUCIÓN:
Al ser $f(x)$ una función polinómica, es continua y derivable en todos los puntos de la recta numérica, luego se cumplen las condiciones de validez del Teorema de Bolzano en todo intervalo de la recta numérica y, en particular, en el intervalo pedido. Observemos que $f(0) \prec 0$ y $f(2) \succ 0$ ( la función toma signos opuestos en los extremos de dicho intervalo ), de lo cual podemos deducir que la gráfica de la función tiene que cortar al eje de abscisas al menos una vez en dicho intervalo, esto es, $f(x)$ posee al menos una raíz comprendida entre $0$ y $2$. $\square$
Determinar los puntos de inflexión y los intervalos de concavidad/convexidad de la siguiente función
Determinar los puntos de inflexión y los intervalos de concavidad/convexidad de la función $f(x)=x^3-2x$
SOLUCIÓN:
En un punto de inflexión se cumple que $f''(x)=0$. Calculando, pues, la segunda derivada ( $f'(x) = 3x^2 \rightarrow f''(x) = 6x$ ) e imponiendo esta condición: $6x = 0 \Leftrightarrow x=0$. Encontramos un sólo punto de inflexión, cuya abscisa es $x=0$; y, por tanto, su ordenada ( valor de función en dicho punto ) es $f(0)=0$. A la izquierda de $x=0$, $f''(x) \prec 0 $, por lo que la función es cóncava en el intervalo $(-\infty\,,\,0)$; a la derecha de $x=0$, $f''(x) \succ 0$, indicando ello que la función es convexa en el intervalo $(0\,,\,\infty)$. $\square$
Demostrar que la siguiente función tiene exactamente una raíz ...
Demostrar que la función $f(x)=x^5+x-5$ tiene exactamente una raíz.
SOLUCIÓN:
Observemos que si intentamos resolver la ecuación $f(x)=0$ para encontrar las raíces de la función pedida, no podemos hacerlo de forma exacta; debería, pues, hacerse de forma aproximada; de ahí la pregunta formulada, aunque no nos piden que encontremos el valor de la raíz sino simplemente se nos pide que justifiquemos la afirmación del enunciado: "la función pedida sólo tiene una raíz". Para ello, vamos a utilizar el Teorema de Rolle y el Teorema de Bolzano.
Según el Teorema de Rolle, el número de raíces de una función continua en un intervalo $[a,b]$ ( en este caso en toda la recta numérica ) y derivable en $(a,b)$ ( en este caso es derivable en toda la recta numérica ) es igual, a lo sumo, al número de ráices de la función derivada más uno. Veamos, pues, cuántas raíces tiene la función derivada
$f'(x)=5x^4+1$; para ello, igualamos a cero y resolvemos la ecuación resultante: $5x^4+1=0$. Esta ecuación no tiene solución en el conjunto de los números reales, por tanto, el número de raíces, $n$, de $f'(x)$ es cero ( $n=0$ ). Entonces, como ya hemos comentado, por el Teorema de Rolle, el máximo número de raíces de $f(x)$ es $n+1$, que en el caso que nos ocupa es $0+1=1$.
Sólo nos queda, ahora, demostrar que existe dicha raíz. Observemos que $f(0)=-5 \prec 0$ y $f(2) \succ 0$, presentado un cambio de signo en el intervalo $[0,2]$, de lo cual deducimos que, al ser continua la función, según el teorema de Bolzano, ésta corta al eje de abscisas al menos en un punto de dicho intervalo. Y como hemos visto, por el Teorema de Rolle, que el número máximo de dichos puntos de corte ( raíces ) es $1$, queda probado que la función pedida tiene exactamente una raíz. $\square$
Demostrar que la siguiente función tiene una sóla raíz ...
Demostrar que la función $f(x)=x^5-5$ tiene exactamente una raíz, sin calcularla explícitamente.
SOLUCIÓN:
La función dada es de tipo polinómico y, por tanto, su dominio de definición es toda la recta real. Veamos si tiene extremos relativos. La condición necesaria para la existencia de dichos puntos es $f'(x)=0$; luego, derivando e igualando a cero: $5x^4=0$, de donde se sigue que sólo hay un extremo relativo: $x=0$. Si empleamos el criterio de la segunda derivada, nos encontramos que en este caso no decide, ya que al ser $f''(x)=20\,x^3$, $f''(0)=0$ ( no es ni positiva ni negativa ). Recurrimos por tanto al criterio de la primera derivada, encontrando que $\text{signo}(f'(0^{-}))=\text{signo}(f'(-1))=\text{signo}(5)$, que es positivo; y $\text{signo}(f'(0^{+}))=\text{signo}(f'(+1))=\text{signo}(5)$, que también es positivo; por tanto, la abscisa $x=0$ corresponde a un punto de inflexión de la gráfica de $f(x)$, luego ésta no puede cortar al eje de abscisas en más de un punto, con lo cual, podemos afirmar que de tener $f(x)$ alguna raíz, sólo puede ser una. Veamos ahora si existe dicha raíz: observemos que $f(1) \prec 0 $ y $f(2) \succ 0$, luego por el Teorema de Bolzano ( $f$ es continua y derivable, en este caso, en todo el dominio de definición ), la gráfica de $f$ corta al eje de abscisas entre $x=1$ y $x=2$. Y por lo dicho anteriormente, este punto de corte tiene que ser único; es decir, $f(x)$ tiene una única raíz ( exactamente una raíz ). $\square$
Calcular la siguiente integral definida ...
Calcular la siguiente integral definida [ aplicar Segundo Teorema Fundamental del Cálculo (TFC2) ] $$\int_{2}^{4}\,(x^2+2x+1)\,dx$$
SOLUCIÓN:
Por el TFC2,
$\int_{2}^{4}\,(x^2+2x+1)\,dx=F(4)-F(2)$ (1)
donde $F(x)$ es una función primitiva de $f(x)=x^2+2x+1=(x+1)^2$; y como en el ejercicio anterior hemos visto que una primitiva de dicha función es $F(x)=\dfrac{1}{3}\,(x+1)^3$, encontramos, de (1), que la integral pedida es $$(4+1)^3-(2+1)^3=125-27=\dfrac{93}{8}$$
$\square$
Calcular la integral indefinida ...
A partir del Primer Teorema Fundamental del Cálculo, calcular la familia de primitivas de la función $f(x)=(x+1)^2$
SOLUCIÓN:
Se nos pide que calculemos la integral indefinida $\int \, f(x)dx$; para ello, debemos encontrar una función $F(x)$ tal que $F'(x)=f(x)$; y, por tanto, $(F(x)+C)'=f(x)$, por ser $C$ una constante arbitraria. Daremos, pues, como respuesta: $F(x)+C$. Vamos a calcularlo:
Haciendo el cambio de variable $u=x+1$ y derivando respecto de $x$: $u'=(x+1)'=1$, luego $\dfrac{du}{dx}=1$; esto es, $du=dx$. Así, $\int \, f(x)dx=\int\,u^2\,du=\dfrac{1}{3}\,u^3+C$; y, deshaciendo el cambio de variable, encontramos que la integral pedida es $\dfrac{1}{3}\,(x+1)^3+C$, donde $C$ es una constante arbitraria.
Comprobación:
$\left( \dfrac{1}{3}\,(x+1)^3+C\right)'=\dfrac{1}{3}\cdot 3 (x+1)^2+0=(x+1)^2$
$\square$
Encontrar los máximos y mínimos locales
Encontrar los máximos y mínimos locales de la función $$f(x)=x^3+2x^2-1$$
SOLUCIÓN:
De existir extremos relativos, la derivada primera debe anularse en dichos puntos. Derivando la función e imponiendo esta condición, $f'(x)=0$,obtenemos $$3x^2+4x=0$$ que resolvemos factorizando el primer miembro $$x(3x+4)=0$$
obteniendo como solución: $0$ y $-\dfrac{4}{3}$
A continuación, analicemos la naturaleza de dichos extremos relativos; para ello, empleamos, en este ejercicio, el criterio de la segunda derivada ( por tratarse $f(x)$ de un polinomio y no presentar dificultad alguna en el cálculo de derivadas ): $$f''(x)=6x+4$$
Así, $f''(0)=6 \cdot 0 +4 = 4 \succ 0$; hay, pues, de un mínimo local ( o mínimo relativo ) en el punto de abscisa $x=0$; su ordenada es $f(0)=-1$. Por otra parte, $f''(-4/3)=-4 \prec 0$, de lo cual deducimos que hay un máximo local ( o máximo relativo ) en el punto de abscisa $x=-4/3$, y su ordenada es $f(-4/3)=5/27$. $\square$
lunes, 11 de mayo de 2015
Determinar las asíntotas de la función ...
Determinar las rectas asíntotas de la función $$f(x)=\dfrac{x^3+x^2+x+1}{x}$$
SOLUCIÓN:
Las rectas asíntotas perpendiculares al eje de abscisas, de ecuación $x=k$, cumplen la siguiente condición $$\displaystyle \lim_{x \rightarrow k}\,f(x)= \pm \infty$$ Observemos que $$\displaystyle \lim_{x \rightarrow 0^{-}}\,f(x)= -\infty$$ y $$\displaystyle \lim_{x \rightarrow 0^{+}}\,f(x)= +\infty$$ encontrando, pues, una recta asíntota ( vertical ) de ecuación $x=0$. Nota: observemos que en $x=0$, la función presenta problemas de definición al anularse ( para dicho valor ) el denominador ( y no el numerador ).
Las recta asíntotas oblícuas ( entre las cuales incluimos las horizontales ) tienen por ecuación $y=mx+k$. La pendiente $m$ se determina mediante el límite $\displaystyle m=\lim_{x \rightarrow \pm \infty}\,f'(x)$ ( la recta asíntota es tangente a la gráfica de la función en el infinito ), que lo mismo que $\displaystyle m=\lim_{x \rightarrow \pm \infty}\,\dfrac{f(x)}{x}$; y, una vez conocido dicho valor, podemos calcular la ordenada en el origen $k$ despejándola de la ecuación ( de la recta asíntota ) a la vez que pasamos al límite ( por operar en el infinito): $\displaystyle k=\lim_{x \rightarrow \pm \infty}\,\left( f(x)-mx \right)$. Observemos que el límite que nos da el valor de $m$ diverge; en efecto, $\displaystyle \lim_{x \rightarrow \infty}\,f'(x)=\lim_{x \rightarrow +\infty}\,(2x+1-\dfrac{1}{x^2})=\infty$, por lo cual concluimos que no existen asíntotas oblícuas. $\square$
Calcular el límite ...
Calcular el siguiente límite $$\displaystyle \lim_{x \rightarrow 0}\, \dfrac{e^x-1}{x}$$
SOLUCIÓN:
Al pasar al límite nos encontramos con una indeterminación del tipo $\dfrac{0}{0}$. Para resolverla, aplicamos la regla de L'Hôpital,
$\displaystyle \lim_{x \rightarrow 0}\, \dfrac{e^x-1}{x}=\lim_{x \rightarrow 0}\, \dfrac{(e^x-1)'}{(x)'}=\lim_{x \rightarrow 0}\, \dfrac{e^x}{1}=e^0=1$
$\square$
jueves, 7 de mayo de 2015
Calcular la integral indefinida ...
Calcular la integral indefinida $$\int\,\dfrac{1+\ln{x}}{x}\,dx$$
SOLUCIÓN:
Mediante el cambio de variable $$t=1+\ln{x}$$
obtenemos ( diferenciando en cada miembro ),
$$dt=\dfrac{1}{x}\,dx$$
por lo que la integral pedida puede escribirse de la forma
$$\int\,t\,dt$$
que es de fácil integración, obteniendo
$$\dfrac{1}{2}\,t^2+C$$
y, deshaciendo el cambio de variable, encontramos la familia de primitivas de la función $\dfrac{1+\ln{x}}{x}$,
$$\dfrac{1}{2}\,(1+\ln{x})^2+C$$
donde $C$ es la constante de integración
$\square$
miércoles, 6 de mayo de 2015
Sistemas de ecuaciones lineales. Método de Gauss Jordan. Ejemplo.
Calcular el límite de la sucesión numérica cuyo término general es ...
Enunciado:
Calcular el límite de la sucesión de números reales, de término general¡
$a_{n}=\sqrt{n}-\sqrt{n+1}$
Solución:
Al pasar al límite
$\displaystyle \lim_{n \rightarrow \infty}\,\sqrt{n}-\sqrt{n+1}$
nos encontramos con una indeterminación del tipo $\infty - \infty$
que resolveremos multiplicando y dividiendo por la expresión conjugada del argumento del límite
$\sqrt{n}+\sqrt{n+1}$
entonces,
$\displaystyle\lim_{n \rightarrow \infty}\,\sqrt{n}-\sqrt{n+1}$
$\displaystyle=\lim_{n \rightarrow \infty}\,\dfrac{\big(\sqrt{n}-\sqrt{n+1}\big)\big(\sqrt{n}+\sqrt{n+1}\big)}{\sqrt{n}+\sqrt{n+1}}$
$\displaystyle=\lim_{n \rightarrow \infty}\,\dfrac{n-(n+1)}{\sqrt{n}+\sqrt{n+1}}$
$\displaystyle=\lim_{n \rightarrow \infty}\,\dfrac{-1}{\sqrt{n}+\sqrt{n+1}}$
$=\dfrac{-1}{\infty}$
$=0$
$\blacksquare$