sábado, 17 de septiembre de 2016
El tiempo, en meses, de permanencia de un socio en un cierto club deportivo, se puede aproximar por una variable aleatoria (...)
ENUNCIADO. El tiempo, en meses, de permanencia de un socio en un cierto club deportivo, se puede aproximar por una variable aleatoria con distribución normal de media desconocida $\mu$ y desviación típica/estándar $\sigma=9$ meses.
a) Se toma una muestra aleatoria simple de $100$ personas que han sido socias de ese club, resultando una estancia media de $\bar{x}=8'1$ meses. Determínese un intervalo de confianza al $90\,\%$ para la media de la población $\mu$
b) Sabiendo que para una muestra aleatoria simple de $144$ personas se ha obtenido el intervalo de confianza $(7'766\,,\,10'233)$ para la media de la población $\mu$, determínese el nivel de confianza con el que se obtuvo dicho intervalo.
SOLUCIÓN.
a)
Denotemos por $X$ a la variable aleatoria de la población "tiempo de permanencia en el club". Sabemos que $X \sim N(\mu\,,\,9)$ ( en meses ), entonces un intervalo de confianza para la estimación de la media de la población $\mu$ es $(\bar{x}-E\,,\,\bar{x}+E)$, donde $\bar{x}=8'1$ meses y $E$ es el máximo error cometido en la estimación ( amplitud del intervalo de confianza ), que viene dado por $E=z_{\alpha/2}\cdot \dfrac{\sigma}{\sqrt{n}}$ y cuyo valor vamos a calcular a continuación. Como el nivel de confianza es $1-\alpha=0{,}90$, luego $\alpha=0{,}10$ y por tanto $\alpha/2=0{,}05$; entonces $P\{Z \le z_{\alpha/2}\}=1-0{,}05=0{,}95$, por lo que consultando en las tablas de la distribución de probabilidad normal tipificada $N(0\,,\,1)$ encontramos el siguiente valor de la abscisa $z_{\alpha/2}\approx 1'64$
Así, $E=1'64 \cdot \dfrac{9}{\sqrt{100}}\approx 1'476$. Y, por consiguiente, el intervalo de confianza pedido para la media de la población es $(8'1-1'476\,,\,8'1+1'476)$ esto es $(6'624\,,\,9'576)$. En buena lógica, vamos ahora a aproximar el extremo inferior por defecto y el extremo superior por exceso, por lo que podemos concluir que el intervalo de confianza pedido es $(6\;,\;10)$ meses.
b)
Recordemos que la amplitud del intervalo de confianza viene dado por $E=z_{\alpha/2}\cdot \dfrac{\sigma}{\sqrt{n}}$. En este apartado del problema, partimos de los siguientes datos: $\sigma=9$ minutos, $n=144$ y $E =\dfrac{10'233-7'766}{2}=1'2335$ minutos. entonces $1'2335=z_{\alpha/2}\cdot \dfrac{9}{\sqrt{144}} \Rightarrow z_{\alpha/2}\approx 1'64$. Consultando ahora las tablas de la función de distribución normal tipificada $N(0,1)$ encontramos $F(1'64) \equiv P\{ Z \le z_{\alpha/2} \}=P\{ Z \le 1'64\}=1-\alpha/2=0'9495$.
Entonces, si $1-\alpha/2=0'9495=94'95\,\%$, el nivel de riesgo en la estimación es $\alpha=2\cdot (1-0'9495)=0'101$, de donde se sigue que el nivel de confianza $1-\alpha$ es igual a $1-0'101=0'899=89'9\,\%$
$\square$
a) Se toma una muestra aleatoria simple de $100$ personas que han sido socias de ese club, resultando una estancia media de $\bar{x}=8'1$ meses. Determínese un intervalo de confianza al $90\,\%$ para la media de la población $\mu$
b) Sabiendo que para una muestra aleatoria simple de $144$ personas se ha obtenido el intervalo de confianza $(7'766\,,\,10'233)$ para la media de la población $\mu$, determínese el nivel de confianza con el que se obtuvo dicho intervalo.
SOLUCIÓN.
a)
Denotemos por $X$ a la variable aleatoria de la población "tiempo de permanencia en el club". Sabemos que $X \sim N(\mu\,,\,9)$ ( en meses ), entonces un intervalo de confianza para la estimación de la media de la población $\mu$ es $(\bar{x}-E\,,\,\bar{x}+E)$, donde $\bar{x}=8'1$ meses y $E$ es el máximo error cometido en la estimación ( amplitud del intervalo de confianza ), que viene dado por $E=z_{\alpha/2}\cdot \dfrac{\sigma}{\sqrt{n}}$ y cuyo valor vamos a calcular a continuación. Como el nivel de confianza es $1-\alpha=0{,}90$, luego $\alpha=0{,}10$ y por tanto $\alpha/2=0{,}05$; entonces $P\{Z \le z_{\alpha/2}\}=1-0{,}05=0{,}95$, por lo que consultando en las tablas de la distribución de probabilidad normal tipificada $N(0\,,\,1)$ encontramos el siguiente valor de la abscisa $z_{\alpha/2}\approx 1'64$
Así, $E=1'64 \cdot \dfrac{9}{\sqrt{100}}\approx 1'476$. Y, por consiguiente, el intervalo de confianza pedido para la media de la población es $(8'1-1'476\,,\,8'1+1'476)$ esto es $(6'624\,,\,9'576)$. En buena lógica, vamos ahora a aproximar el extremo inferior por defecto y el extremo superior por exceso, por lo que podemos concluir que el intervalo de confianza pedido es $(6\;,\;10)$ meses.
b)
Recordemos que la amplitud del intervalo de confianza viene dado por $E=z_{\alpha/2}\cdot \dfrac{\sigma}{\sqrt{n}}$. En este apartado del problema, partimos de los siguientes datos: $\sigma=9$ minutos, $n=144$ y $E =\dfrac{10'233-7'766}{2}=1'2335$ minutos. entonces $1'2335=z_{\alpha/2}\cdot \dfrac{9}{\sqrt{144}} \Rightarrow z_{\alpha/2}\approx 1'64$. Consultando ahora las tablas de la función de distribución normal tipificada $N(0,1)$ encontramos $F(1'64) \equiv P\{ Z \le z_{\alpha/2} \}=P\{ Z \le 1'64\}=1-\alpha/2=0'9495$.
Entonces, si $1-\alpha/2=0'9495=94'95\,\%$, el nivel de riesgo en la estimación es $\alpha=2\cdot (1-0'9495)=0'101$, de donde se sigue que el nivel de confianza $1-\alpha$ es igual a $1-0'101=0'899=89'9\,\%$
$\square$
Para efectuar un diagnóstico (...)
ENUNCIADO. Para efectuar cierto diagnóstico, un hospital dispone de dos escáneres, a los que denotamos por $A$ y $B$. El $65\,\%$ de las pruebas de diagnóstico que se llevan a cabo en ese hospital se realizan usando el escáner $A$, el resto con el escáner $B$. Se sabe además que el diagnóstico efectuado usando el escáner $A$ es erróneo en un $5\,\%$ de los casos, mientras que el diagnóstico efectuado usando el escáner $B$ es erróneo en un $8\,\%$ de los casos. Calcúlese la probabilidad de que:
a) El diagnóstico correspondiente a una prueba ( elegida al azar ) efectuada a un paciente en ese hospital sea erróneo
b) El diagnóstico se haya efectuado usando el escáner $A$, sabiendo que ha sido erróneo.
SOLUCIÓN.
a)
Denotemos por $E$ al suceso aleatorio "realizar una prueba errónea"; y, por $A$ y $B$, a los sucesos aleatorios "hacer una prueba con el escáner $A$" y "hacer una prueba con el escáner $B$", respectivamente. Entonces, $$E=(E \cap A)\cup (E \cap B)$$ y como los sucesos $E \cap A$ y $E \cap B$ son incompatibles ( su intersección es vacía ), podemos escribir $$P(E)=P(E \cap A)+P(E \cap B)$$ Ahora bien, por la definición de probabilidad de sucesos condicionados, $P(E \cap A)=P(E|A)P(A)$ y $P(E \cap B)=P(E|B)P(B)$ luego $$P(E)=P(E|A)P(A)+P(E|B)P(B) \quad \text{(teorema de la Probabilidad Total)}$$ Poniendo pues los datos, llegamos a $$P(E)=0,65\cdot 0,05 + 0,35\cdot 0,08=0,0605$$
b)
Por el teorema de Bayes, podemos escribir $$P(A|E)=\dfrac{P(E|A)P(A)}{P(E)}$$ y con los datos de que disponemos, $$P(A|E)=\dfrac{0,65\cdot 0,05}{0,0605}\approx 0,2893$$
$\square$
a) El diagnóstico correspondiente a una prueba ( elegida al azar ) efectuada a un paciente en ese hospital sea erróneo
b) El diagnóstico se haya efectuado usando el escáner $A$, sabiendo que ha sido erróneo.
SOLUCIÓN.
a)
Denotemos por $E$ al suceso aleatorio "realizar una prueba errónea"; y, por $A$ y $B$, a los sucesos aleatorios "hacer una prueba con el escáner $A$" y "hacer una prueba con el escáner $B$", respectivamente. Entonces, $$E=(E \cap A)\cup (E \cap B)$$ y como los sucesos $E \cap A$ y $E \cap B$ son incompatibles ( su intersección es vacía ), podemos escribir $$P(E)=P(E \cap A)+P(E \cap B)$$ Ahora bien, por la definición de probabilidad de sucesos condicionados, $P(E \cap A)=P(E|A)P(A)$ y $P(E \cap B)=P(E|B)P(B)$ luego $$P(E)=P(E|A)P(A)+P(E|B)P(B) \quad \text{(teorema de la Probabilidad Total)}$$ Poniendo pues los datos, llegamos a $$P(E)=0,65\cdot 0,05 + 0,35\cdot 0,08=0,0605$$
b)
Por el teorema de Bayes, podemos escribir $$P(A|E)=\dfrac{P(E|A)P(A)}{P(E)}$$ y con los datos de que disponemos, $$P(A|E)=\dfrac{0,65\cdot 0,05}{0,0605}\approx 0,2893$$
$\square$
Se considera la función (...)
ENUNCIADO. Se considera la función real de variable real $$f(x)=\dfrac{x^2-3}{x^2-9}$$
a) Calcúlense sus asíntotas
b) Determínense los intervalos de crecimiento y decrecimiento de la función
SOLUCIÓN.
a)
Podemos expresar la función de la forma $$f(x)=\dfrac{x^2-3}{(x-3)(x+3)}$$ con lo cual vemos que el denominador ( y no el numerador ) se anula para $x=-3$ y $x=3$, así que la función tiene dos asíntotas verticales: $$\text{a.v}_1:x=-3$$ y $$\text{a.v}_2:x=3$$ Veamos ahora si tiene alguna asíntota oblicua ( incluidas las posibles asíntotas horizontales en ese grupo ).
Una asíntota oblicua se escribe de la forma $y=mx+k$, donde $$\displaystyle m\overset{\text{def}}{=}\lim_{x \rightarrow \pm \infty}\,f'(x)=\lim_{x \rightarrow \pm \infty}\,\dfrac{f(x)}{x}$$ Así, $\displaystyle m=\lim_{x \rightarrow \pm \infty}\,\dfrac{x^2-3}{x(x-3)(x+3)}=0$ por ser el grado del polinomio del denominador mayor que el del polinomio del numerador. La única asíntota que encontramos, pues, es una asíntota horizontal, del tipo $y=k$.
Procedemos a calcular el valor de $k$: $\displaystyle k\overset{\text{def}}{=}\lim_{x \rightarrow \pm \infty}\,(f(x)-mx)=\lim_{x \rightarrow \pm \infty}\,f(x)=\lim_{x \rightarrow \pm \infty}\,\dfrac{x^2-3}{x^2-9}=1$, por ser iguales los grados de los polinomios del numerador y denominador, siendo los coeficientes de mayor grado igual a $1$ en sendos polinomios. Por consiguiente, la ecuación de la recta asíntota horizontal que acabamos de encontrar es $\text{a.h.}:y=1$
b)
Para calcular los intervalos de crecimiento y decrecimiento, vamos a ver primero si la función tiene algún extremo relativo. Imponiendo la condición necesaria de existencia de extremos relativos $$f'(x)=0$$ vemos que $$\dfrac{2x(x^2-9)-2x(x^2-3)}{(x^2-9)^2}=0 \Leftrightarrow x=0$$ Investiguemos ahora de qué tipo de extremo relativo se trata. A la izquierda de $x^*=0$, en puntos muy cercanos ( pongamos que, por ejemplo, en $x=-1$) la primera derivada tiene signo positivo; y, a la derecha, en puntos muy cercanos ( por ejemplo en $x=1$ ) tiene signo negativo, de lo cual se deduce que el extremo relativo encontrado corresponde a un máximo relativo.
Con la información recogida hasta este punto podemos ver que $$\displaystyle \lim_{x \rightarrow -3^{-}}\,f(x)=+\infty$$ $$\displaystyle \lim_{x \rightarrow -3^{+}}\,f(x)=-\infty$$ $$\displaystyle \lim_{x \rightarrow 3^{-}}\,f(x)=-\infty$$ y $$\displaystyle \lim_{x \rightarrow 3^{+}}\,f(x)=+\infty$$
También es útil conocer el valor de las raíces de la función: $$f(x)=0 \Leftrightarrow x^2-3=0 \Leftrightarrow x=\left\{\begin{matrix}-\sqrt{3}\\ \\ \sqrt{3}\end{matrix}\right.$$
Así, podemos bosquejar el siguiente gráfico para la función:
con lo cual podemos escribir los intervalos de crecimiento: $(-\infty,-3)$ y $(-3,0)$, así como los de decrecimiento: $(0,3)$ y $(3,+\infty)$
$\square$
a) Calcúlense sus asíntotas
b) Determínense los intervalos de crecimiento y decrecimiento de la función
SOLUCIÓN.
a)
Podemos expresar la función de la forma $$f(x)=\dfrac{x^2-3}{(x-3)(x+3)}$$ con lo cual vemos que el denominador ( y no el numerador ) se anula para $x=-3$ y $x=3$, así que la función tiene dos asíntotas verticales: $$\text{a.v}_1:x=-3$$ y $$\text{a.v}_2:x=3$$ Veamos ahora si tiene alguna asíntota oblicua ( incluidas las posibles asíntotas horizontales en ese grupo ).
Una asíntota oblicua se escribe de la forma $y=mx+k$, donde $$\displaystyle m\overset{\text{def}}{=}\lim_{x \rightarrow \pm \infty}\,f'(x)=\lim_{x \rightarrow \pm \infty}\,\dfrac{f(x)}{x}$$ Así, $\displaystyle m=\lim_{x \rightarrow \pm \infty}\,\dfrac{x^2-3}{x(x-3)(x+3)}=0$ por ser el grado del polinomio del denominador mayor que el del polinomio del numerador. La única asíntota que encontramos, pues, es una asíntota horizontal, del tipo $y=k$.
Procedemos a calcular el valor de $k$: $\displaystyle k\overset{\text{def}}{=}\lim_{x \rightarrow \pm \infty}\,(f(x)-mx)=\lim_{x \rightarrow \pm \infty}\,f(x)=\lim_{x \rightarrow \pm \infty}\,\dfrac{x^2-3}{x^2-9}=1$, por ser iguales los grados de los polinomios del numerador y denominador, siendo los coeficientes de mayor grado igual a $1$ en sendos polinomios. Por consiguiente, la ecuación de la recta asíntota horizontal que acabamos de encontrar es $\text{a.h.}:y=1$
b)
Para calcular los intervalos de crecimiento y decrecimiento, vamos a ver primero si la función tiene algún extremo relativo. Imponiendo la condición necesaria de existencia de extremos relativos $$f'(x)=0$$ vemos que $$\dfrac{2x(x^2-9)-2x(x^2-3)}{(x^2-9)^2}=0 \Leftrightarrow x=0$$ Investiguemos ahora de qué tipo de extremo relativo se trata. A la izquierda de $x^*=0$, en puntos muy cercanos ( pongamos que, por ejemplo, en $x=-1$) la primera derivada tiene signo positivo; y, a la derecha, en puntos muy cercanos ( por ejemplo en $x=1$ ) tiene signo negativo, de lo cual se deduce que el extremo relativo encontrado corresponde a un máximo relativo.
Con la información recogida hasta este punto podemos ver que $$\displaystyle \lim_{x \rightarrow -3^{-}}\,f(x)=+\infty$$ $$\displaystyle \lim_{x \rightarrow -3^{+}}\,f(x)=-\infty$$ $$\displaystyle \lim_{x \rightarrow 3^{-}}\,f(x)=-\infty$$ y $$\displaystyle \lim_{x \rightarrow 3^{+}}\,f(x)=+\infty$$
También es útil conocer el valor de las raíces de la función: $$f(x)=0 \Leftrightarrow x^2-3=0 \Leftrightarrow x=\left\{\begin{matrix}-\sqrt{3}\\ \\ \sqrt{3}\end{matrix}\right.$$
Así, podemos bosquejar el siguiente gráfico para la función:
$\square$
Se considera la función real de variable real (...)
ENUNCIADO. Se considera la función real de variable real $$f(x)=\left\{\begin{matrix}x^2+2x & \text{si} & x \prec 0 \\ -x^2+3x & \text{si} & x \ge 0 \end{matrix}\right.$$
a) Estúdiese la continuidad y la derivabilidad de la función
b) Determínense los valores de $a \in \mathbb{R}$ para los cuales la pendiente de la recta tangente a la gráfica de $f(x)$ en el punto de abscisa $x=a$ es $-2$. Calcúlese, para cada valor de $a$ obtenido, la recta tangente a la gráfica de $f(x)$ en el punto de abscisa $x=a$
SOLUCIÓN.
a)
Estudio de la continuidad:
Las dos tramos polinómicos en que está definida la función son continuos, por ser polinomios. El único punto donde podría haber problemas de continuidad es en $x=0$, sin embargo la función también es continua en dicho punto. En efecto, $\displaystyle \lim_{x\rightarrow 0^-}f(x)=\displaystyle \lim_{x\rightarrow 0^+}f(x)=0$, luego el límite global existe y su valor es $\displaystyle \lim_{x\rightarrow 0}f(x)=0$; y, por otra parte, el valor de dicho límite es igual al valor de la función en $x=0$, $f(0)=0$. En consecuencia la función es continua en todos los puntos del dominio de definición, que es todo el conjunto $\mathbb{R}$.
Estudio de la derivabilidad:
Los dos tramos de la función son derivables en todos los puntos, ya que son polinomios. El único punto que podría presentar problemas de derivabilidad es en $x=0$ ( en punto de engarce de los dos tramos ). Veamos si la función es derivable en $x=0$. Para que lo sea, al calcular los límites que definen la derivada, por la izquierda y por la derecha de $x=0$, deberían dar el mismo valor. Veamos si es así: $$\displaystyle \lim_{\Delta x\rightarrow 0}\dfrac{f(0)-f(0-\Delta x)}{\Delta x}=(x^2+2x)'|_{x=0}=(2x+2)'|_{x=0}=2\cdot 0+2=2$$ por el contrario $$\displaystyle \lim_{\Delta x\rightarrow 0}\dfrac{f(0+\Delta x)-f(0)}{\Delta x}=(-x^2+3x)'|_{x=0}=(-2x+3)'|_{x=0}=-2\cdot 0+3=3$$ Al no coincidir dichos límites, no existe la derivada de $f(x)$ en $x=0$; en otras palabras, no podemos trazar la recta tangente a la gráfica de la función en el punto $x=0$. Así pues, el dominio de derivabilidad de $f(x)$ es $\mathbb{R}\setminus \{0\}$
b)
Procedemos a investigar en qué puntos de $\mathbb{R}$ la recta tangente a la gráfica de la función tiene pendiente negativa. El primer tramo de la función, esto es el polinomio $x^2+2x$ ( definido para todos los números reales negativos ) presenta un mínimo relativo en $x=-1$, ya que ésta es la abscisa del vértice de la parábola dada por dicho polinomio. Por otra parte, el segundo tramo, $-x^2+3x$, que también es un polinomio ( definido para el cero y todos los números reales positivos ) presenta un máximo relativo ( la parábola asociada a dicho tramo polinómico tiene coeficiente principal negativo ) en $x=3/2$, que es la abscisa el vértice de dicha parábola. Nota: También podemos deducir las abscisas de dichos extremos relativos, derivando e igualando a cero.
Entonces, los intervalos de decrecimiento de la función, donde la pendiente de la recta tangente es negativa, son: $I_1=(-\infty,-1)$ e $I_2=(3/2,+\infty)$, con lo cual encontraremos dos valores, $a$, del dominio de derivabilidad de $f(x)$ que cumplen que la pendiente de la recta tangente a la gráfica de la función $f(x)$ es igual a $-2$; uno de ellos ha de ser menor que $-1$, pues está en $I_1$, y el otro ha de ser mayor que $3/2$, pues está en $I_2$. Distinguimos pues los siguientes casos.
Caso I:
La pendiente de la recta tangente en un punto $x=a$ situado a la izquierda de $-1$ ( esto es, del intervalor $I_1$ ) ha de ser igual a $-2$ (enunciado), y dicho valor corresponde a la derivada de la función en dicho punto, $f'(a)$. Como para $x\prec -1$, $f'(x)=2x+2$, tenemos que $(2x+2)_{x=a}=-2$ y por tanto $$2a+2=-2$$ de donde deducimos que $a=-2$
A continuación, vamos a escribir la ecuación de la recta tangente a la gráfica de la función en dicho punto $a=-2$, que designaremos por $\text{r.t.}_1$. Sabemos que la ecuación de dicha recta es de la forma $y=mx+k$, y como la pendiente de dicha recta es $m=-2$, nos queda $y=-2x+k$. Para determinar el valor de la ordenada en el origen, $k$, debemos tener en cuenta que el valor de dicha función lineal afín en $x=a=-2$ ha de coincidir con el valor de la función $f(x)$ en $x=a=-2$. Es decir, $$-2\cdot (-2)+k=f(-2)$$ y como $f(-2)=(-2)^2+2\cdot (-2)=4-4=0$, tenemos que $$-2\cdot (-2)+k=0 \Leftrightarrow k=-4$$ Así que
$$\text{r.t.}_1:y=-2x-4$$
Caso II:
La pendiente de la recta tangente en un punto $x=a$ situado a la izquierda de $3/2$ ( esto es, del intervalor $I_2$ ) ha de ser igual a $-2$ (enunciado ), y dicho valor corresponde a la derivada de la función en dicho punto, $f'(a)$. Como para $x \succ 3/2$, $f'(x)=-2x+3$, tenemos que $(-2x+3)_{x=a}=-2$ y por tanto $$-2a+3=-2$$ de donde deducimos que $a=5/2$
Procedemos a escribir la ecuación de la recta tangente a la gráfica de la función en dicho punto $a=5/2$, que designaremos por $\text{r.t.}_2$. Repetimos los mismos pasos que en el caso I. Sabemos que la ecuación de dicha recta es de la forma $y=mx+k$, y como la pendiente de dicha recta es $m=-2$, nos queda $y=-2x+k$. Para determinar el valor de la ordenada en el origen, $k$, debemos tener en cuenta que el valor de dicha función lineal afín en $x=a=5/2$ ha de coincidir con el valor de la función $f(x)$ en $x=a=5/2$. Es decir, $$-2\cdot \dfrac{5}{2}+k=f(5/2)$$ y como $f(5/2)=-(5/2)^2+3\cdot (5/2)=5/4$, tenemos que $$-2\cdot (5/2)+k=5/4 \Leftrightarrow k=25/4$$ Así que
$$\text{r.t.}_2:y=-2x+\dfrac{25}{4}$$
$\square$
a) Estúdiese la continuidad y la derivabilidad de la función
b) Determínense los valores de $a \in \mathbb{R}$ para los cuales la pendiente de la recta tangente a la gráfica de $f(x)$ en el punto de abscisa $x=a$ es $-2$. Calcúlese, para cada valor de $a$ obtenido, la recta tangente a la gráfica de $f(x)$ en el punto de abscisa $x=a$
SOLUCIÓN.
a)
Estudio de la continuidad:
Las dos tramos polinómicos en que está definida la función son continuos, por ser polinomios. El único punto donde podría haber problemas de continuidad es en $x=0$, sin embargo la función también es continua en dicho punto. En efecto, $\displaystyle \lim_{x\rightarrow 0^-}f(x)=\displaystyle \lim_{x\rightarrow 0^+}f(x)=0$, luego el límite global existe y su valor es $\displaystyle \lim_{x\rightarrow 0}f(x)=0$; y, por otra parte, el valor de dicho límite es igual al valor de la función en $x=0$, $f(0)=0$. En consecuencia la función es continua en todos los puntos del dominio de definición, que es todo el conjunto $\mathbb{R}$.
Estudio de la derivabilidad:
Los dos tramos de la función son derivables en todos los puntos, ya que son polinomios. El único punto que podría presentar problemas de derivabilidad es en $x=0$ ( en punto de engarce de los dos tramos ). Veamos si la función es derivable en $x=0$. Para que lo sea, al calcular los límites que definen la derivada, por la izquierda y por la derecha de $x=0$, deberían dar el mismo valor. Veamos si es así: $$\displaystyle \lim_{\Delta x\rightarrow 0}\dfrac{f(0)-f(0-\Delta x)}{\Delta x}=(x^2+2x)'|_{x=0}=(2x+2)'|_{x=0}=2\cdot 0+2=2$$ por el contrario $$\displaystyle \lim_{\Delta x\rightarrow 0}\dfrac{f(0+\Delta x)-f(0)}{\Delta x}=(-x^2+3x)'|_{x=0}=(-2x+3)'|_{x=0}=-2\cdot 0+3=3$$ Al no coincidir dichos límites, no existe la derivada de $f(x)$ en $x=0$; en otras palabras, no podemos trazar la recta tangente a la gráfica de la función en el punto $x=0$. Así pues, el dominio de derivabilidad de $f(x)$ es $\mathbb{R}\setminus \{0\}$
b)
Procedemos a investigar en qué puntos de $\mathbb{R}$ la recta tangente a la gráfica de la función tiene pendiente negativa. El primer tramo de la función, esto es el polinomio $x^2+2x$ ( definido para todos los números reales negativos ) presenta un mínimo relativo en $x=-1$, ya que ésta es la abscisa del vértice de la parábola dada por dicho polinomio. Por otra parte, el segundo tramo, $-x^2+3x$, que también es un polinomio ( definido para el cero y todos los números reales positivos ) presenta un máximo relativo ( la parábola asociada a dicho tramo polinómico tiene coeficiente principal negativo ) en $x=3/2$, que es la abscisa el vértice de dicha parábola. Nota: También podemos deducir las abscisas de dichos extremos relativos, derivando e igualando a cero.
Entonces, los intervalos de decrecimiento de la función, donde la pendiente de la recta tangente es negativa, son: $I_1=(-\infty,-1)$ e $I_2=(3/2,+\infty)$, con lo cual encontraremos dos valores, $a$, del dominio de derivabilidad de $f(x)$ que cumplen que la pendiente de la recta tangente a la gráfica de la función $f(x)$ es igual a $-2$; uno de ellos ha de ser menor que $-1$, pues está en $I_1$, y el otro ha de ser mayor que $3/2$, pues está en $I_2$. Distinguimos pues los siguientes casos.
Caso I:
La pendiente de la recta tangente en un punto $x=a$ situado a la izquierda de $-1$ ( esto es, del intervalor $I_1$ ) ha de ser igual a $-2$ (enunciado), y dicho valor corresponde a la derivada de la función en dicho punto, $f'(a)$. Como para $x\prec -1$, $f'(x)=2x+2$, tenemos que $(2x+2)_{x=a}=-2$ y por tanto $$2a+2=-2$$ de donde deducimos que $a=-2$
A continuación, vamos a escribir la ecuación de la recta tangente a la gráfica de la función en dicho punto $a=-2$, que designaremos por $\text{r.t.}_1$. Sabemos que la ecuación de dicha recta es de la forma $y=mx+k$, y como la pendiente de dicha recta es $m=-2$, nos queda $y=-2x+k$. Para determinar el valor de la ordenada en el origen, $k$, debemos tener en cuenta que el valor de dicha función lineal afín en $x=a=-2$ ha de coincidir con el valor de la función $f(x)$ en $x=a=-2$. Es decir, $$-2\cdot (-2)+k=f(-2)$$ y como $f(-2)=(-2)^2+2\cdot (-2)=4-4=0$, tenemos que $$-2\cdot (-2)+k=0 \Leftrightarrow k=-4$$ Así que
$$\text{r.t.}_1:y=-2x-4$$
Caso II:
La pendiente de la recta tangente en un punto $x=a$ situado a la izquierda de $3/2$ ( esto es, del intervalor $I_2$ ) ha de ser igual a $-2$ (enunciado ), y dicho valor corresponde a la derivada de la función en dicho punto, $f'(a)$. Como para $x \succ 3/2$, $f'(x)=-2x+3$, tenemos que $(-2x+3)_{x=a}=-2$ y por tanto $$-2a+3=-2$$ de donde deducimos que $a=5/2$
Procedemos a escribir la ecuación de la recta tangente a la gráfica de la función en dicho punto $a=5/2$, que designaremos por $\text{r.t.}_2$. Repetimos los mismos pasos que en el caso I. Sabemos que la ecuación de dicha recta es de la forma $y=mx+k$, y como la pendiente de dicha recta es $m=-2$, nos queda $y=-2x+k$. Para determinar el valor de la ordenada en el origen, $k$, debemos tener en cuenta que el valor de dicha función lineal afín en $x=a=5/2$ ha de coincidir con el valor de la función $f(x)$ en $x=a=5/2$. Es decir, $$-2\cdot \dfrac{5}{2}+k=f(5/2)$$ y como $f(5/2)=-(5/2)^2+3\cdot (5/2)=5/4$, tenemos que $$-2\cdot (5/2)+k=5/4 \Leftrightarrow k=25/4$$ Así que
$$\text{r.t.}_2:y=-2x+\dfrac{25}{4}$$
$\square$
Se considera el sistema de ecuaciones (...)
ENUNCIADO. Se considera el sistema de ecuaciones dependientes del parámetro real $a$ $$\left\{\begin{matrix}(a-1)x&+&y&+&z&=&1 \\ x&+&(a-1)y&+&(a-1)z&=&1 \\ x&&&+&az&=&1 \end{matrix}\right.$$
a) Discútase el sistema según los valores de $a$
b) Resuélvase el sistema para $a=3$
SOLUCIÓN.
a)
Reduciendo el sistema por Gauss,
$\left\{\begin{matrix}(a-1)x&+&y&+&z&=&1 \\ x&+&(a-1)y&+&(a-1)z&=&1 \\ x&&&+&az&=&1 \end{matrix}\right.$
$\sim \left\{\begin{matrix}y&+&(a-1)x&+&z&=&1 \\ (a-1)y&+&x&+&(a-1)z&=&1 \\ &&x&+&az&=&1 \end{matrix}\right. \overset{-(a-1)e_1+e_2\rightarrow e_2}{\sim}$
$\sim \left\{\begin{matrix}y&+&(a-1)x&+&z&=&1 \\ &&a(a-2)x&&&=&(a-2) \\ &&x&+&az&=&1 \end{matrix}\right.$
$\sim \left\{\begin{matrix}y&+&(a-1)x&+&z&=&1 \\ &&x&+&az&=&1 \\ &&a(a-2)x&&&=&(a-2) \end{matrix}\right.$
$\sim \left\{\begin{matrix}y&+&z&+&(a-1)x&=&1 \\ &&az&+&x&=&1 \\ &&&&a(a-2)x&=&(a-2) \end{matrix}\right.$
Debemos distinguir ahora los siguientes casos:
Caso 1. Si $a=0$, la tercera ecuación conduce a una contradicción, $0=-2$, con lo cual el sistema es incompatible para este valor del parámetro.
Caso 2. Si $a=2$, la tercera ecuación es trivial, pues obtenemos $0=0$, luego el sistema tiene dos ecuaciones independientes, con lo cual el rango del mismo es $r=2$; y como el número de incógnitas es $n=3$, el sistema es compatible indeterminado con $n-r=3-2=1$ variable secundaria ( y $2$ variables principales ), según el teorema de Rouché-Fröbenius.
Caso 3. Si $a \notin \{0,2\}$, el sistema es compatible determinado, ya que $r=n=3$ ( por el teorema de Rouché-Fröbenius )
b)
Si $a=3$, como $3 \notin \{0,2\}$, estamos en el caso 3 y el sistema es compatible determinado. El sistema equivalente reducido es
$ \left\{\begin{matrix}y&+&z&+&2x&=&1 \\ &&3z&+&x&=&1 \\ &&&&3x&=&1 \end{matrix}\right.$
Despejando $x$ de la tercera ecuación, obtenemos $$x=1/3$$ sustituyendo este valor en la segunda ecuación y despejando $z$ obtenemos, $$z=2/9$$ y sustituyendo los dos valores encontrados para $x$ y $z$ en la primera ecuación y despejando $y$, se llega a $$y=1/9$$
$\square$
a) Discútase el sistema según los valores de $a$
b) Resuélvase el sistema para $a=3$
SOLUCIÓN.
a)
Reduciendo el sistema por Gauss,
$\left\{\begin{matrix}(a-1)x&+&y&+&z&=&1 \\ x&+&(a-1)y&+&(a-1)z&=&1 \\ x&&&+&az&=&1 \end{matrix}\right.$
$\sim \left\{\begin{matrix}y&+&(a-1)x&+&z&=&1 \\ (a-1)y&+&x&+&(a-1)z&=&1 \\ &&x&+&az&=&1 \end{matrix}\right. \overset{-(a-1)e_1+e_2\rightarrow e_2}{\sim}$
$\sim \left\{\begin{matrix}y&+&(a-1)x&+&z&=&1 \\ &&a(a-2)x&&&=&(a-2) \\ &&x&+&az&=&1 \end{matrix}\right.$
$\sim \left\{\begin{matrix}y&+&(a-1)x&+&z&=&1 \\ &&x&+&az&=&1 \\ &&a(a-2)x&&&=&(a-2) \end{matrix}\right.$
$\sim \left\{\begin{matrix}y&+&z&+&(a-1)x&=&1 \\ &&az&+&x&=&1 \\ &&&&a(a-2)x&=&(a-2) \end{matrix}\right.$
Debemos distinguir ahora los siguientes casos:
Caso 1. Si $a=0$, la tercera ecuación conduce a una contradicción, $0=-2$, con lo cual el sistema es incompatible para este valor del parámetro.
Caso 2. Si $a=2$, la tercera ecuación es trivial, pues obtenemos $0=0$, luego el sistema tiene dos ecuaciones independientes, con lo cual el rango del mismo es $r=2$; y como el número de incógnitas es $n=3$, el sistema es compatible indeterminado con $n-r=3-2=1$ variable secundaria ( y $2$ variables principales ), según el teorema de Rouché-Fröbenius.
Caso 3. Si $a \notin \{0,2\}$, el sistema es compatible determinado, ya que $r=n=3$ ( por el teorema de Rouché-Fröbenius )
b)
Si $a=3$, como $3 \notin \{0,2\}$, estamos en el caso 3 y el sistema es compatible determinado. El sistema equivalente reducido es
$ \left\{\begin{matrix}y&+&z&+&2x&=&1 \\ &&3z&+&x&=&1 \\ &&&&3x&=&1 \end{matrix}\right.$
Despejando $x$ de la tercera ecuación, obtenemos $$x=1/3$$ sustituyendo este valor en la segunda ecuación y despejando $z$ obtenemos, $$z=2/9$$ y sustituyendo los dos valores encontrados para $x$ y $z$ en la primera ecuación y despejando $y$, se llega a $$y=1/9$$
$\square$
El tiempo, en minutos, que los empleados de unos grandes almacenes tardan en (...)
ENUNCIADO. El tiempo, en minutos, que los empleados de unos grandes almacenes tardan en llegar a su casa se puede aproximar por una variable aleatoria con distribución normal, de media $\mu$ desconocida y desviación típica/estándar $\sigma=5$ minutos. Se pide:
a) Se toma una muestra aleatoria simple de $64$ empleados y su media muestral resulta ser $\bar{x}=30$ minutos. Determínese un intervalo de confianza al $95\,\%$ para $\mu$
b) ¿ Qué tamaño mínimo debe tener una muestra aleatoria simple para que el correspondiente intervalo de confianza para $\mu$, al $99\,\%$, tenga una amplitud a lo sumo de $1$ minuto ?
SOLUCIÓN.
a)
Denotemos por $X$ a la variable aleatoria de la población "tiempo en llegar a casa". Sabemos que $X \sim N(\mu\,,\,5)$, entonces un intervalo de confianza para la estimación de la media de la población $\mu$ es $(\bar{x}-E\,,\,\bar{x}+E)$, donde $\bar{x}=30$ minutos y $E$ es el máximo error cometido en la estimación, que viene dado por $E=z_{\alpha/2}\cdot \dfrac{\sigma}{\sqrt{n}}$ y cuyo valor vamos a calcular a continuación: como el nivel de confianza es $1-\alpha=0'95$, $\alpha=0'05$ y por tanto $\alpha/2=0'025$; entonces $P\{Z \le z_{\alpha/2}\}=1-0'025=0'975$, por lo que consultando en las tablas de la distribución de probabilidad $N(0\,,\,1)$ encontramos el siguiente valor de la abscisa $z_{\alpha/2}=1'96$
Así, $E=1'96 \cdot \dfrac{5}{\sqrt{64}}=1'225$. Y, por consiguiente, el intervalo de confianza pedido para la media de la población es $(30-1'225\,,\,30+1'225)$ esto es $(28'775\,,\,31'225)$, intervalo que, en buena lógica, podemos aproximar a $(28\;,\;32)$ minutos.
b)
El intervalo de confianza de la media poblacional $\mu$, es $(\bar{x}-E\,,\,\bar{x}+E)$. Y la amplitud de dicho intervalo viene dada por $E=z_{\alpha/2}\cdot \dfrac{\sigma}{\sqrt{n}}$. Como, en este caso, $\sigma=5$ minutos, y $E \le 1$ minuto, entonces $z_{\alpha/2}\cdot \dfrac{5}{\sqrt{n}} \le 1$
Por otra parte, si $1-\alpha=0'99$, entonces $\alpha=0'01$, luego $\displaystyle P\{Z \le z_{\alpha/2}\}=1-z_{\alpha/2}$. En nuestro caso, $P\{Z \le z_{0'01/2}\}=1-0'005=0'995$, por lo que, consultando las tablas de la función de distribución de la variable aleatoria normal tipificada $Z \sim N(0,1)$, encontramos $z_{\alpha/2}=z_{0'01/2} \overset{\text{tablas}}{\approx} 2'58$
Podemos escribir ahora que $2'58\cdot \dfrac{5}{\sqrt{n}} \le 1$, así que elevando al cuadrado ambos miembros de la desigualdad resulta $n \ge \big( \dfrac{2'58 \cdot 5)}{1}\big)^2 \approx 167$ ( aproximando por exceso ), luego el tamaño mínimo de la muestra es $n_{\text{mín}} = 167$
$\square$
a) Se toma una muestra aleatoria simple de $64$ empleados y su media muestral resulta ser $\bar{x}=30$ minutos. Determínese un intervalo de confianza al $95\,\%$ para $\mu$
b) ¿ Qué tamaño mínimo debe tener una muestra aleatoria simple para que el correspondiente intervalo de confianza para $\mu$, al $99\,\%$, tenga una amplitud a lo sumo de $1$ minuto ?
SOLUCIÓN.
a)
Denotemos por $X$ a la variable aleatoria de la población "tiempo en llegar a casa". Sabemos que $X \sim N(\mu\,,\,5)$, entonces un intervalo de confianza para la estimación de la media de la población $\mu$ es $(\bar{x}-E\,,\,\bar{x}+E)$, donde $\bar{x}=30$ minutos y $E$ es el máximo error cometido en la estimación, que viene dado por $E=z_{\alpha/2}\cdot \dfrac{\sigma}{\sqrt{n}}$ y cuyo valor vamos a calcular a continuación: como el nivel de confianza es $1-\alpha=0'95$, $\alpha=0'05$ y por tanto $\alpha/2=0'025$; entonces $P\{Z \le z_{\alpha/2}\}=1-0'025=0'975$, por lo que consultando en las tablas de la distribución de probabilidad $N(0\,,\,1)$ encontramos el siguiente valor de la abscisa $z_{\alpha/2}=1'96$
Así, $E=1'96 \cdot \dfrac{5}{\sqrt{64}}=1'225$. Y, por consiguiente, el intervalo de confianza pedido para la media de la población es $(30-1'225\,,\,30+1'225)$ esto es $(28'775\,,\,31'225)$, intervalo que, en buena lógica, podemos aproximar a $(28\;,\;32)$ minutos.
b)
El intervalo de confianza de la media poblacional $\mu$, es $(\bar{x}-E\,,\,\bar{x}+E)$. Y la amplitud de dicho intervalo viene dada por $E=z_{\alpha/2}\cdot \dfrac{\sigma}{\sqrt{n}}$. Como, en este caso, $\sigma=5$ minutos, y $E \le 1$ minuto, entonces $z_{\alpha/2}\cdot \dfrac{5}{\sqrt{n}} \le 1$
Por otra parte, si $1-\alpha=0'99$, entonces $\alpha=0'01$, luego $\displaystyle P\{Z \le z_{\alpha/2}\}=1-z_{\alpha/2}$. En nuestro caso, $P\{Z \le z_{0'01/2}\}=1-0'005=0'995$, por lo que, consultando las tablas de la función de distribución de la variable aleatoria normal tipificada $Z \sim N(0,1)$, encontramos $z_{\alpha/2}=z_{0'01/2} \overset{\text{tablas}}{\approx} 2'58$
Podemos escribir ahora que $2'58\cdot \dfrac{5}{\sqrt{n}} \le 1$, así que elevando al cuadrado ambos miembros de la desigualdad resulta $n \ge \big( \dfrac{2'58 \cdot 5)}{1}\big)^2 \approx 167$ ( aproximando por exceso ), luego el tamaño mínimo de la muestra es $n_{\text{mín}} = 167$
$\square$
Sean dos sucesos aleatorios (...)
ENUNCIADO. Sean $A$ y $B$ dos sucesos de un experimento aleatorio tales que $P(A)=3/4$, $P(A|B)=3/4$ y $P(B|A)=1/4$
a) Demuéstrese que $A$ y $B$ son sucesos independientes pero no incompatibles
b) Calcúlese $P(\bar{A}|\bar{B})$
NOTA: $\bar{S}$ denota el suceso complementario/contrario del suceso $S$
SOLUCIÓN.
a)
Los sucesos $A$ y $B$ son compatibles:
Para demostrar que $A$ y $B$ son compatibles debemos probar que $P(A \cup B) \neq P(A)+P(B)$; en otras palabras, y teniendo en cuenta la propiedad general $P(A \cup B)=P(A)+P(B)-P(A \cap B)$, es necesario probar que $P(A \cap B) \neq 0$. Para ello consideremos las siguientes expresiones que vienen de la definición de probabilidad condicionada: $$P(A|B)\overset{\text{def}}{=}\dfrac{P(A \cap B}{P(B)} \quad \quad (1)$$ y $$P(B|A)\overset{\text{def}}{=}\dfrac{P(B \cap A}{P(A)}=\dfrac{P(A \cap B}{P(A)} \quad \quad (2)$$ Dividiendo, miembro a miembro, (1) entre (2), obtenemos $$\dfrac{P(A|B)}{P(B|A)}=\dfrac{P(A)}{P(B)}$$ de donde se deduce que $$P(B)=\dfrac{P(A)P(B|A)}{P(A|B)}=\dfrac{(3/4)\cdot (1/4)}{1/4}=1/4$$ Entonces $$P(A \cap B)\overset{\text(1)}{=}P(A|B)P(B)=\dfrac{3}{4}\cdot \dfrac{1}{4}=\dfrac{3}{16} \neq 0$$
$\square$
Los sucesos $A$ y $B$ son independientes:
De la definición de independencia de sucesos sabemos que $A$ y $B$ son independientes si y sólo si se cumplen las siguientes condiciones: $P(A|B)=P(A)$ y $P(B|A)=P(B)$. En efecto, con los datos del problema y los resultados obtenidos se comprueba que $P(A|B)=P(A)=\dfrac{3}{4}$ y $P(B|A)=P(B)=\dfrac{1}{4}$
Otra forma de demostrarlo es la siguiente. Los sucesos $A$ y $B$ son independientes si se cumple la siguiente igualdad $P(A \cap B)=P(A)P(B)$ ( consecuencia de la definición de sucesos independientes ). Bastará pues comprobar que, con los datos del problema y los resultados que acabamos de obtener, ésto se cumple. En efecto, hemos calculado el valor del primer miembro de la igualdad en la primera parte: $P(A \cap B)=\dfrac{3}{16}$; y, también, se ha calculado $P(B)$ que es $\dfrac{1}{4}$. Entonces, como sabemos ( enunciado ) que $P(A)=\dfrac{3}{4}$, se cumple que $P(A)P(B)=\dfrac{3}{4}\cdot \dfrac{1}{4}=\dfrac{3}{16}$
b)
Sabemos que $$P(\bar{A}|\bar{B})\overset{\text{def. cond.}}{=}\dfrac{P(\bar{A}\cap \bar{B})}{P(\bar{B})}$$ Ahora bien, de la primera ley de Morgan, $
\bar{A}\cap \bar{B}=\overline{A \cup B}$, por tanto $$P(\bar{A}|\bar{B})=\dfrac{P(\overline{A \cup B})}{P(\bar{B})}=\dfrac{1-P(A\cup B)}{1-P(B)} \quad \quad (3)$$ y, por la fórmula de inclusión-exclusión $$P(A \cup B)=P(A)+P(B)-P(A\cap B)$$ Con los datos del problema encontramos: $$P(A \cup B)=1-\dfrac{3}{4}-\dfrac{1}{4}+\dfrac{3}{16}=\dfrac{3}{16}$$ y $$1-P(B)=1-\dfrac{1}{4}=\dfrac{3}{4}$$ Y sustituyendo estos resultados en (3), obtenemos $$P(\bar{A}|\bar{B})=\dfrac{3/16}{3/4}=\dfrac{1}{4}$$
$\square$
a) Demuéstrese que $A$ y $B$ son sucesos independientes pero no incompatibles
b) Calcúlese $P(\bar{A}|\bar{B})$
NOTA: $\bar{S}$ denota el suceso complementario/contrario del suceso $S$
SOLUCIÓN.
a)
Los sucesos $A$ y $B$ son compatibles:
Para demostrar que $A$ y $B$ son compatibles debemos probar que $P(A \cup B) \neq P(A)+P(B)$; en otras palabras, y teniendo en cuenta la propiedad general $P(A \cup B)=P(A)+P(B)-P(A \cap B)$, es necesario probar que $P(A \cap B) \neq 0$. Para ello consideremos las siguientes expresiones que vienen de la definición de probabilidad condicionada: $$P(A|B)\overset{\text{def}}{=}\dfrac{P(A \cap B}{P(B)} \quad \quad (1)$$ y $$P(B|A)\overset{\text{def}}{=}\dfrac{P(B \cap A}{P(A)}=\dfrac{P(A \cap B}{P(A)} \quad \quad (2)$$ Dividiendo, miembro a miembro, (1) entre (2), obtenemos $$\dfrac{P(A|B)}{P(B|A)}=\dfrac{P(A)}{P(B)}$$ de donde se deduce que $$P(B)=\dfrac{P(A)P(B|A)}{P(A|B)}=\dfrac{(3/4)\cdot (1/4)}{1/4}=1/4$$ Entonces $$P(A \cap B)\overset{\text(1)}{=}P(A|B)P(B)=\dfrac{3}{4}\cdot \dfrac{1}{4}=\dfrac{3}{16} \neq 0$$
$\square$
Los sucesos $A$ y $B$ son independientes:
De la definición de independencia de sucesos sabemos que $A$ y $B$ son independientes si y sólo si se cumplen las siguientes condiciones: $P(A|B)=P(A)$ y $P(B|A)=P(B)$. En efecto, con los datos del problema y los resultados obtenidos se comprueba que $P(A|B)=P(A)=\dfrac{3}{4}$ y $P(B|A)=P(B)=\dfrac{1}{4}$
Otra forma de demostrarlo es la siguiente. Los sucesos $A$ y $B$ son independientes si se cumple la siguiente igualdad $P(A \cap B)=P(A)P(B)$ ( consecuencia de la definición de sucesos independientes ). Bastará pues comprobar que, con los datos del problema y los resultados que acabamos de obtener, ésto se cumple. En efecto, hemos calculado el valor del primer miembro de la igualdad en la primera parte: $P(A \cap B)=\dfrac{3}{16}$; y, también, se ha calculado $P(B)$ que es $\dfrac{1}{4}$. Entonces, como sabemos ( enunciado ) que $P(A)=\dfrac{3}{4}$, se cumple que $P(A)P(B)=\dfrac{3}{4}\cdot \dfrac{1}{4}=\dfrac{3}{16}$
b)
Sabemos que $$P(\bar{A}|\bar{B})\overset{\text{def. cond.}}{=}\dfrac{P(\bar{A}\cap \bar{B})}{P(\bar{B})}$$ Ahora bien, de la primera ley de Morgan, $
\bar{A}\cap \bar{B}=\overline{A \cup B}$, por tanto $$P(\bar{A}|\bar{B})=\dfrac{P(\overline{A \cup B})}{P(\bar{B})}=\dfrac{1-P(A\cup B)}{1-P(B)} \quad \quad (3)$$ y, por la fórmula de inclusión-exclusión $$P(A \cup B)=P(A)+P(B)-P(A\cap B)$$ Con los datos del problema encontramos: $$P(A \cup B)=1-\dfrac{3}{4}-\dfrac{1}{4}+\dfrac{3}{16}=\dfrac{3}{16}$$ y $$1-P(B)=1-\dfrac{1}{4}=\dfrac{3}{4}$$ Y sustituyendo estos resultados en (3), obtenemos $$P(\bar{A}|\bar{B})=\dfrac{3/16}{3/4}=\dfrac{1}{4}$$
$\square$
Dada la función real de variable real (...)
ENUNCIADO. Dada la función real de variable real definida por $$f(x)=\left\{\begin{matrix}x^2+1 & \text{si} & x < 1 \\ \\ \dfrac{ax+b}{x} & \text{si} & 1 \le x \le 2 \\ \\ \sqrt{x^3+1} & \text{si} & x > 2\end{matrix}\right.$$
a) Determínense los valores que deben tomar los parámetros $a$ y $b$ para que $f(x)$ sea continua en $x=1$ y $x=2$
b) Calcúlese, para $a=4$ y $b=-2$, el área del recinto acotado por la gráfica de $f(x)$, el eje de abscisas y las rectas $x=1$ y $x=2$
SOLUCIÓN.
a)
Para que $f(x)$ sea continua en $x=1$ ha de cumplirse $$\{x^2+1:x=1\}=\{\dfrac{ax+b}{x}:x=1\}$$ y por tanto $$a+b=2 \quad \quad \quad (1)$$
Para que $f(x)$ sea continua en $x=2$ ha de cumplirse $$\{\sqrt{x^3+1}:x=2\}=\{\dfrac{ax+b}{x}:x=2\}$$ y por tanto $$2a+b=6 \quad \quad \quad (2)$$
Resolviendo ahora el sistema de ecuaciones que forman (1) y (2) $$\left\{\begin{matrix}a&+&b&=&2 \\ 2a&+&b&=&6\end{matrix}\right. \overset{e_2-e_1 \rightarrow e_2}{\sim} \left\{\begin{matrix}a&+&b&=&2 \\ a&&&=&4\end{matrix}\right. \sim \left\{\begin{matrix}&&b&=&-2 \\ a&&&=&4\end{matrix}\right. $$
b)
$$\displaystyle \text{Área}=\left|\int_{1}^{2}\,\dfrac{4x-2}{x}\,dx\right|$$ Teniendo en cuenta que una primitiva, $F(x)$, de la función $\dfrac{4x-2}{x}$ es $\displaystyle \int \dfrac{4x-2}{x} dx = 4\int dx -2 \int \dfrac{1}{x}dx = 4x-2\,\ln x$, podemos escribir $$\displaystyle \text{Área}\overset{\text{Barrow}}{=}\left|F(2)-F(1)\right|=(4\cdot 2 - 2\,\ln 2)-(4\cdot 1 - 2 \ln 1)=4-2\ln2=2\,(2-\ln2)$$
$\square$
a) Determínense los valores que deben tomar los parámetros $a$ y $b$ para que $f(x)$ sea continua en $x=1$ y $x=2$
b) Calcúlese, para $a=4$ y $b=-2$, el área del recinto acotado por la gráfica de $f(x)$, el eje de abscisas y las rectas $x=1$ y $x=2$
SOLUCIÓN.
a)
Para que $f(x)$ sea continua en $x=1$ ha de cumplirse $$\{x^2+1:x=1\}=\{\dfrac{ax+b}{x}:x=1\}$$ y por tanto $$a+b=2 \quad \quad \quad (1)$$
Para que $f(x)$ sea continua en $x=2$ ha de cumplirse $$\{\sqrt{x^3+1}:x=2\}=\{\dfrac{ax+b}{x}:x=2\}$$ y por tanto $$2a+b=6 \quad \quad \quad (2)$$
Resolviendo ahora el sistema de ecuaciones que forman (1) y (2) $$\left\{\begin{matrix}a&+&b&=&2 \\ 2a&+&b&=&6\end{matrix}\right. \overset{e_2-e_1 \rightarrow e_2}{\sim} \left\{\begin{matrix}a&+&b&=&2 \\ a&&&=&4\end{matrix}\right. \sim \left\{\begin{matrix}&&b&=&-2 \\ a&&&=&4\end{matrix}\right. $$
b)
$$\displaystyle \text{Área}=\left|\int_{1}^{2}\,\dfrac{4x-2}{x}\,dx\right|$$ Teniendo en cuenta que una primitiva, $F(x)$, de la función $\dfrac{4x-2}{x}$ es $\displaystyle \int \dfrac{4x-2}{x} dx = 4\int dx -2 \int \dfrac{1}{x}dx = 4x-2\,\ln x$, podemos escribir $$\displaystyle \text{Área}\overset{\text{Barrow}}{=}\left|F(2)-F(1)\right|=(4\cdot 2 - 2\,\ln 2)-(4\cdot 1 - 2 \ln 1)=4-2\ln2=2\,(2-\ln2)$$
$\square$
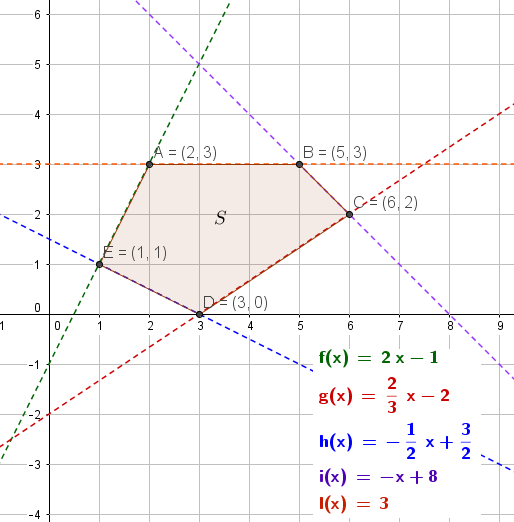
Sea la región del plano dada por el sistema de desigualdades (...)
ENUNCIADO. Sea $S$ la región del plano definida por $$\left\{\begin{matrix}2x&-&y&\ge&1 \\ 2x&-&3y&\le&6 \\ x&+&2y&\ge&3 \\ x&+&y&\le&8 \\ &&y&\le&3\end{matrix}\right.$$
a) Represéntese la region $S$ y calcúlense las coordenadas de sus vértices
b) Obténganse los valores máximo y mínimo de la función $f(x,y)=2x+y$ en la región $S$, indicando los puntos en los cuales se alcanzan dichos valores máximo y mínimo.
SOLUCIÓN.
a)
Podemos expresar la desigualdades de la siguiente forma $$\left\{\begin{matrix} y \le 2x-1 \\ y \ge \dfrac{2}{3}x-2 \\ y \ge -\dfrac{1}{2}x+\dfrac{3}{2}\\ y \le -x+8 \\ y \le 3\end{matrix}\right.$$ que es más conveniente para encontrar la región $S$ ( convexa ) del plano.
Las ecuaciones de las rectas que contienen los lados de dicha región son $$\left\{\begin{matrix} y = 2x-1 \\ y = \dfrac{2}{3}x-2 \\ y = -\dfrac{1}{2}x+\dfrac{3}{2}\\ y = -x+8 \\ y = 3\end{matrix}\right.$$
Representando dichas rectas en el plano y calculando los puntos de intersección de las mismas ( vértices de la región convexa $S$ ) obtenemos
b)
Despejando la variable dependiente $y$ de $f(x,y)\equiv k=2x+y$ se obtiene $y=-2x+k$, que representa una recta del haz de rectas paralelas de la función objetivo. El valor máximo ( respectivamente, mínimo ) de la ordenada en el origen $k$ es pues el valor máximo ( respectivamente, mínimo ) de $f$. Tal como se muestra en las siguientes figuras, hemos encontrado que el máximo corresponde a la recta del haz que pasa por $C(6,2)$, que es igual a $f(6,2)=14$; y, el mínimo, a la recta del haz que pasa por $E(1,1)$, y su valor es $f(1,1)=3$
$\square$
a) Represéntese la region $S$ y calcúlense las coordenadas de sus vértices
b) Obténganse los valores máximo y mínimo de la función $f(x,y)=2x+y$ en la región $S$, indicando los puntos en los cuales se alcanzan dichos valores máximo y mínimo.
SOLUCIÓN.
a)
Podemos expresar la desigualdades de la siguiente forma $$\left\{\begin{matrix} y \le 2x-1 \\ y \ge \dfrac{2}{3}x-2 \\ y \ge -\dfrac{1}{2}x+\dfrac{3}{2}\\ y \le -x+8 \\ y \le 3\end{matrix}\right.$$ que es más conveniente para encontrar la región $S$ ( convexa ) del plano.
Las ecuaciones de las rectas que contienen los lados de dicha región son $$\left\{\begin{matrix} y = 2x-1 \\ y = \dfrac{2}{3}x-2 \\ y = -\dfrac{1}{2}x+\dfrac{3}{2}\\ y = -x+8 \\ y = 3\end{matrix}\right.$$
Representando dichas rectas en el plano y calculando los puntos de intersección de las mismas ( vértices de la región convexa $S$ ) obtenemos
b)
Despejando la variable dependiente $y$ de $f(x,y)\equiv k=2x+y$ se obtiene $y=-2x+k$, que representa una recta del haz de rectas paralelas de la función objetivo. El valor máximo ( respectivamente, mínimo ) de la ordenada en el origen $k$ es pues el valor máximo ( respectivamente, mínimo ) de $f$. Tal como se muestra en las siguientes figuras, hemos encontrado que el máximo corresponde a la recta del haz que pasa por $C(6,2)$, que es igual a $f(6,2)=14$; y, el mínimo, a la recta del haz que pasa por $E(1,1)$, y su valor es $f(1,1)=3$
$\square$
Se considera la matriz (...)
ENUNCIADO. Se considera la matriz $$A=\begin{pmatrix}k & -1 & 0 \\ -7 & k & k \\ -1 & -1 & k \end{pmatrix}$$
a) Estúdiese para qué valores del parámetro real $k$ la matriz $A$ tiene inversa
b) Determínese, para $k=1$, la matriz $X$ tal que $XA=\text{Id}$
NOTA: $\text{Id}$ denota la matriz identidad de tamaño $3 \times 3 $
SOLUCIÓN.
a)
$A$ tiene inversa si y sólo si $\text{det}(A)\neq 0$. Entonces, $$\begin{vmatrix}k & -1 & 0 \\ 7 & k & k \\ -1 & -1 & k \end{vmatrix}\overset{[1]}{=}(-1)\cdot \begin{vmatrix}-1 & 0 \\ k & k \end{vmatrix}-(-1)\cdot \begin{vmatrix}k & 0 \\ 7 & k \end{vmatrix}=k^2+k=0 \Leftrightarrow k \in \{-1,0\}$$ luego $A$ tiene inversa si y sólo si $k \notin \{-1,0\}$
[1] Desarrollando por los adjuntos de la tercera fila
b)
Como $k=1 \notin \{-1,0\}$, podemos afirmar que $A=\begin{pmatrix}1 & -1 & 0 \\ -7 & 1 & 1 \\ -1 & -1 & 1 \end{pmatrix}$ tiene inversa. Entonces, si $XA=\text{Id}$, $A=X^{-1}$. Procedemos a calcular la matriz inversa de $A$ por el método de reducción de Gauss-Jordan, que es muy eficiente. Se trata de transformar $(A|\text{Id})$ en $(\text{Id}|A^{-1})$, mediante operaciones elementales entre filas.
$\left(\begin{array}{ccc|ccc} 1 & -1 & 0 & 1 & 0 & 0 \\ -7 & 1 & 1 & 0 & 1 & 0 \\ -1 & -1 & 1 & 0 & 0 & 1 \end{array}\right) \overset{f_1+f_3 \rightarrow f_3; 7f_1+f_2 \rightarrow f_2}{\rightarrow} \left(\begin{array}{ccc|ccc} 1 & -1 & 0 & 1 & 0 & 0 \\ 0 & -6 & 1 & 7 & 1 & 0 \\ 0 & -2 & 1 & 1 & 0 & 1 \end{array}\right) \rightarrow$
$\overset{(-1/3)f_2+f_3 \rightarrow f_3}{\rightarrow} \left(\begin{array}{ccc|ccc} 1 & -1 & 0 & 1 & 0 & 0 \\ 0 & -6 & 1 & 7 & 1 & 0 \\ 0 & 0 & 2/3 & -4/3 & -1/3 & 1 \end{array}\right) \rightarrow$
$\overset{(-3/2)f_3+f_2 \rightarrow f_2}{\rightarrow} \left(\begin{array}{ccc|ccc} 1 & -1 & 0 & 1 & 0 & 0 \\ 0 & -6 & 0 & 9 & 3/2 & -3/2 \\ 0 & 0 & 2/3 & -4/3 & -1/3 & 1 \end{array}\right) \rightarrow$
$\overset{(-1/6)f_2+f_1 \rightarrow f_1}{\rightarrow} \left(\begin{array}{ccc|ccc} 1 & 0 & 0 & -1/2 & -1/4 & 1/4 \\ 0 & -6 & 0 & 9 & 3/2 & -3/2 \\ 0 & 0 & 2/3 & -4/3 & -1/3 & 1 \end{array}\right) \rightarrow$
$\overset{(-1/6)f_2\rightarrow f_2;(3/2)f_3 \rightarrow f_3}{\rightarrow} \left(\begin{array}{ccc|ccc} 1 & 0 & 0 & -1/2 & -1/4 & 1/4 \\ 0 & 1 & 0 & -3/2 & -1/4 & -1/4 \\ 0 & 0 & 1 & -2 & -1/2 & 3/2 \end{array}\right)$
Por consiguiente $$A^{-1}=\left(\begin{array}{ccc} -1/2 & -1/4 & 1/4 \\ -3/2 & -1/4 & -1/4 \\ -2 & -1/2 & 3/2 \end{array}\right)$$
$\square$
a) Estúdiese para qué valores del parámetro real $k$ la matriz $A$ tiene inversa
b) Determínese, para $k=1$, la matriz $X$ tal que $XA=\text{Id}$
NOTA: $\text{Id}$ denota la matriz identidad de tamaño $3 \times 3 $
SOLUCIÓN.
a)
$A$ tiene inversa si y sólo si $\text{det}(A)\neq 0$. Entonces, $$\begin{vmatrix}k & -1 & 0 \\ 7 & k & k \\ -1 & -1 & k \end{vmatrix}\overset{[1]}{=}(-1)\cdot \begin{vmatrix}-1 & 0 \\ k & k \end{vmatrix}-(-1)\cdot \begin{vmatrix}k & 0 \\ 7 & k \end{vmatrix}=k^2+k=0 \Leftrightarrow k \in \{-1,0\}$$ luego $A$ tiene inversa si y sólo si $k \notin \{-1,0\}$
[1] Desarrollando por los adjuntos de la tercera fila
b)
Como $k=1 \notin \{-1,0\}$, podemos afirmar que $A=\begin{pmatrix}1 & -1 & 0 \\ -7 & 1 & 1 \\ -1 & -1 & 1 \end{pmatrix}$ tiene inversa. Entonces, si $XA=\text{Id}$, $A=X^{-1}$. Procedemos a calcular la matriz inversa de $A$ por el método de reducción de Gauss-Jordan, que es muy eficiente. Se trata de transformar $(A|\text{Id})$ en $(\text{Id}|A^{-1})$, mediante operaciones elementales entre filas.
$\left(\begin{array}{ccc|ccc} 1 & -1 & 0 & 1 & 0 & 0 \\ -7 & 1 & 1 & 0 & 1 & 0 \\ -1 & -1 & 1 & 0 & 0 & 1 \end{array}\right) \overset{f_1+f_3 \rightarrow f_3; 7f_1+f_2 \rightarrow f_2}{\rightarrow} \left(\begin{array}{ccc|ccc} 1 & -1 & 0 & 1 & 0 & 0 \\ 0 & -6 & 1 & 7 & 1 & 0 \\ 0 & -2 & 1 & 1 & 0 & 1 \end{array}\right) \rightarrow$
$\overset{(-1/3)f_2+f_3 \rightarrow f_3}{\rightarrow} \left(\begin{array}{ccc|ccc} 1 & -1 & 0 & 1 & 0 & 0 \\ 0 & -6 & 1 & 7 & 1 & 0 \\ 0 & 0 & 2/3 & -4/3 & -1/3 & 1 \end{array}\right) \rightarrow$
$\overset{(-3/2)f_3+f_2 \rightarrow f_2}{\rightarrow} \left(\begin{array}{ccc|ccc} 1 & -1 & 0 & 1 & 0 & 0 \\ 0 & -6 & 0 & 9 & 3/2 & -3/2 \\ 0 & 0 & 2/3 & -4/3 & -1/3 & 1 \end{array}\right) \rightarrow$
$\overset{(-1/6)f_2+f_1 \rightarrow f_1}{\rightarrow} \left(\begin{array}{ccc|ccc} 1 & 0 & 0 & -1/2 & -1/4 & 1/4 \\ 0 & -6 & 0 & 9 & 3/2 & -3/2 \\ 0 & 0 & 2/3 & -4/3 & -1/3 & 1 \end{array}\right) \rightarrow$
$\overset{(-1/6)f_2\rightarrow f_2;(3/2)f_3 \rightarrow f_3}{\rightarrow} \left(\begin{array}{ccc|ccc} 1 & 0 & 0 & -1/2 & -1/4 & 1/4 \\ 0 & 1 & 0 & -3/2 & -1/4 & -1/4 \\ 0 & 0 & 1 & -2 & -1/2 & 3/2 \end{array}\right)$
Por consiguiente $$A^{-1}=\left(\begin{array}{ccc} -1/2 & -1/4 & 1/4 \\ -3/2 & -1/4 & -1/4 \\ -2 & -1/2 & 3/2 \end{array}\right)$$
$\square$
martes, 6 de septiembre de 2016
Suscribirse a:
Entradas (Atom)